يعتبر نموذج الانحدار اللوجستي واحد من أهم النماذج الإحصائية لنمذجة إحتمالية وجود فئة معينة أو حدث معين مثل النجاح / الفشل. وذلك نظرا لأن الانحدار اللوجستي يستخدم عدة متغيرات مُتوقَّعة والتي يمكن أن تكون مستمرة أو فئوية. يمكن توسيع هذا لنمذجة عدة فئات من الأحداث مثل تحديد ما إذا كانت الصورة تحتوي على قط أو نمر أو سمك ، وما إلى ذلك. سيتم تعيين احتمال بين 0 و 1 لكل كائن يتم اكتشافه في الصورة ، بحيث يكون المجموع الكلي يساوي واحد. يعرف الانحدار اللوجستي أيضا بتسميات أخرى كنموذج لوجيت (Logit) أو المصنف العام للأنتروبية. يندرج الانحدار اللوجستي ضمن خوارزميات التعلم الآلي الخاضع للإشراف المخصصة لمهام التصنيف. اكتسب على مدى العقدين الماضيين إهتمام خاص خاصة في القطاع المالي بسبب قدرته البارزة في الكشف عن المختلسين. أدناه مخطط للإستخدام العام للانحدار اللوجستي وغيره من المصنفات الخطية الشائعة.

كيف يعمل نموذج الانحدار اللوجستي
يظهر للوهلة الاولى عند قراءة إسم النموذج التناقض عندما نقول أن النموذج يستخدم للتصنيف و في نفس الوقت يحتوي إسمه على مصطلح “الانحدار”. لكن هذا هو السبب في أن الانحدار اللوجستي هو نموذج يستحق الاهتمام. حيث أنه يستخدام معادلة الانحدار الخطي لتوقع مخرجات ثنائية منفصلة. علاوة على ذلك، يتم تصنيفه ضمن “نماذج التمييز” لطرق تعلم الآلة مثل خوارزمية الة المتجه الدعم SVM و خوارزمية Perceptron ANN حيث تستخدم جميعها المعادلات الخطية ككتلة بناء وتحاول زيادة جودة المخرجات في بيانات التدريب.
لفهم كيفية عمل خوارزمية الانحدار اللوجستي يجب في البداية الاجابة عن الأسئلة التالية:
- ما تعريف التصنيف؟
- لماذا لا يتم إستخدم الانحدار الخطي لحل مهام التصنيف؟
- ماهي خوارزمية الانحدار اللوجستي؟
- ما هي حدود القرار؟
- كيف نتتحقق من أداء النموذج؟
ما تعريف التصنيف؟
في البداية تعرف أي مشكلة كمشكلة تصنيف عندما تكون المتغيرات المستقلة مستمرة بطبيعتها ويكون المتغير التابع على شكل فئوي. بمعنى اخر، أي في فئات مثل الفئة أ او الفئة ب. على سبيل المثال ، مهمة تصنيف البريد الإلكتروني على أنه بريد عشوائي أم لا. أيضا تصنيف الورم على أنه خبيث أو حميد ، وكذلك تصنيف المعاملة المالية على أنها احتيالية أو حقيقية. جميع إجابات هذه المشكلات تكون على شكل فئوي ، أي ب نعم أو لا. أحيانا قد نواجه مهام تصنيف تكون النتاتج المتوقعة فيها أكثر من فئتين و تُعرف هذه الأنواع من المهام بمهام التصنيف متعددة الفئات.
لماذا لا يتم إستخدم الانحدار الخطي لحل مهام التصنيف؟
لنفترض مثلا أن لدينا بيانات عن نوع الورم (ورم حميد او ورم خبيث) و ذلك استنادا الى حجم الورم. نظرًا لأنها تعتبر مهمة تصنيف ، إذا قمنا برسم البيانات على منحنى بياني، يمكننا أن نرى أن جميع القيم على تقع اما على 0 او على 1. وإذا قمنا بملائمة أفضل خط انحدار ، بافتراض الحد الأدنى عند 0.5 ، فيمكننا القيام بعمل خط معقول.
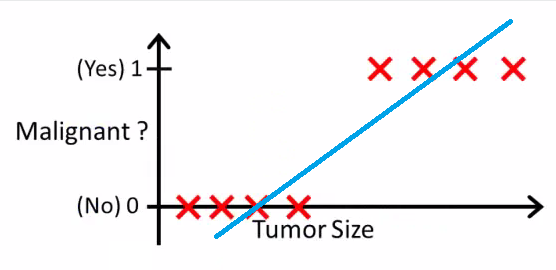
يمكننا تحديد النقطة الموجودة على المحور الافقي حيث تقع جميع القيم على جانبها الأيسر تعتبر فئة سالبة وجميع القيم الموجودة على جانبها الأيمن هي فئة موجبة.
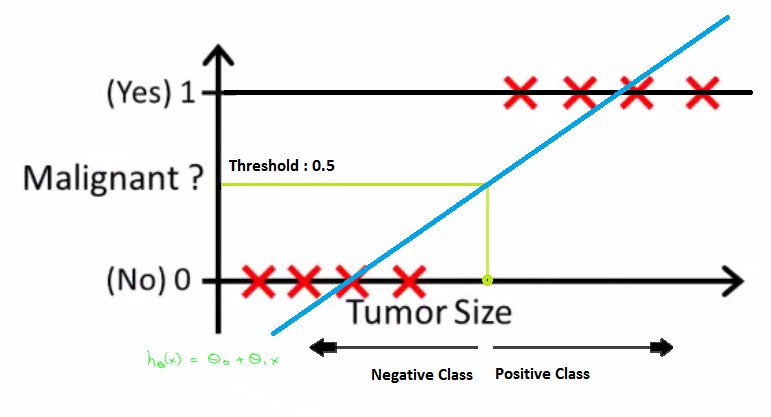
ولكن ماذا لو كان هناك قيم متطرفة في البيانات. ستصبح الأمور فوضوية جدًا. على سبيل المثال الشكل الموضح أدناه:
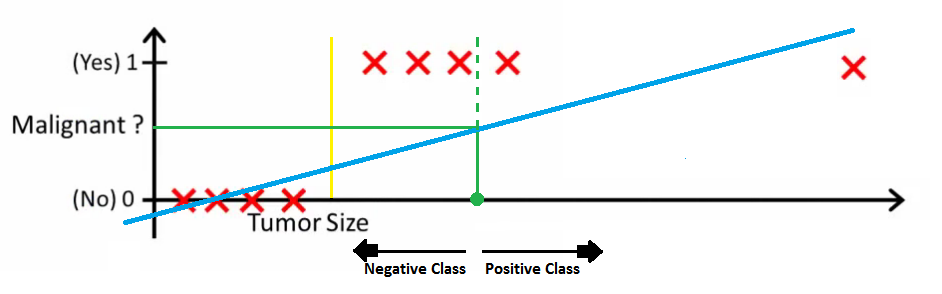
إذا طبقنا أفضل خط انحدار تم العثور عليه ، فلن يكون كافياً لتحديد أي نقطة يمكننا من خلالها التمييز بين الفئات. سيضع بعض العينات ذات الصفة الإيجابية في فئة العينات ذات الصفة السلبية. الخط الأخضر المنقط (حدود القرار) في حالة وجود القيم المتطرفة حيث يقسم الأورام الخبيثة عن الأورام الحميدة مع نسبة خطأ كبيرة. و ذلك يتجلى بوضوح في مدى بعد الخط الاخضر عن الخط الأصفر الذي يقسم بوضوح العينات الإيجابية و السلبية. لذا فإن مجرد قيمة شاذة واحدة قد تخرب توقعات الانحدار الخطي بأكمله. وهذا هو الموضع الذي تظهر فيه أهمية الانحدار اللوجستي.
ماهي خوارزمية الانحدار اللوجستي؟
كما تم مناقشته سابقًا ، للتعامل مع القيم المتطرفة ، يستخدم الانحدار اللوجستي الدالة السينية. و يمكن أن يبدأ تفسير الانحدار اللوجستي بشرح الدالة اللوجستية القياسية. الدالة اللوجستية هي الدالة السينية sigmoid function ، و التي تأخذ أي قيمة حقيقية بين صفر و واحد. يتم تعريفها رياضيا على الشكل التالي
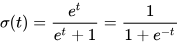
وإذا رسمناها بيانيا ، فسيكون الرسم البياني على شكل منحنى حرف S لذلك تسمى بالدالة السينية
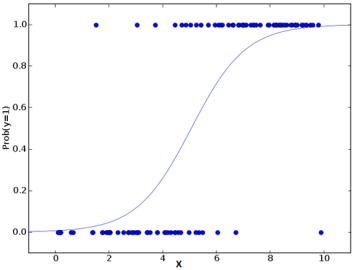
لنفكر في t كدالة خطية في نموذج الانحدار أحادي المتغير
![]()
لذلك ستصبح المعادلة اللوجستية على الشكل التالي
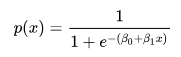
الآن ، عندما يصادف نموذج الانحدار اللوجستي بيانات شاذة ، فسوف يتعامل معها.
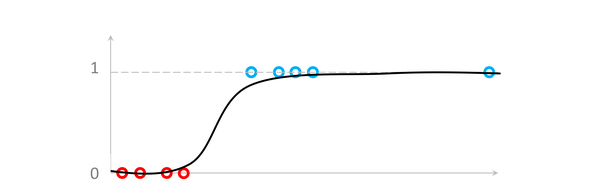
لكن في بعض الأحيان ستحول محورها العمودي إلى اليسار أو اليمين اعتمادًا على كمية وجود القيم المتطرفة.
ما هي حدود القرار؟
أما فيما يتعلق بأهمية حدود القرار فهي تبرز في المساعدة على التفريق بين الاحتمالات إلى عينات موجبة و عينات سالبة.
حدود القرار الخطي
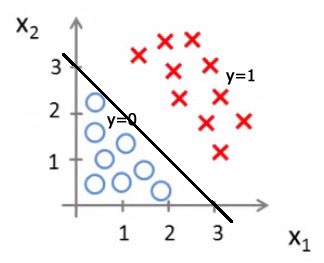

حدود القرار الغير خطي
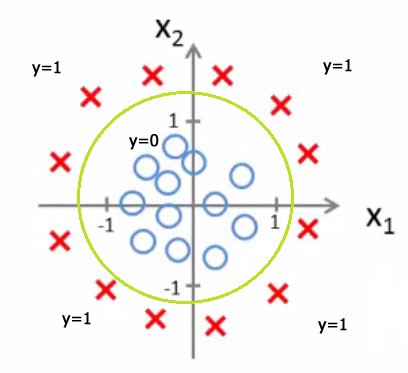
كيف نتتحقق من أداء نموذج الانحدار اللوجستي؟
أما بالنسبة للتحقق من اداء نموذجنا فيمكننا التأكد من ذلك باستخدام مصفوفة الارتباك confusion matrix و منحنى AUC – ROC.
مزايا و عيوب الخوارزمية
| المزايا | العيوب |
|---|---|
|
الانحدار اللوجستي أسهل في التنفيذ والتفسير والتدريب الفعال للغاية |
إذا كان عدد الملاحظات أقل من عدد الميزات ، فلا ينبغي استخدام الانحدار اللوجستي ، وإلا فقد يؤدي إلى فرط مشكلة فرط التخصيص |
|
لا يقدم أي افتراضات حول توزيعات الفئات في حدود الميزة |
يبني حدود خطية |
|
يمكن أن يتوسع بسهولة إلى فئات متعددة (الانحدار متعدد الحدود) ووجهة نظر احتمالية طبيعية للتنبؤات الفئوية |
القيد الرئيسي للانحدار اللوجستي هو افتراض الخطية بين المتغير التابع و المتغيرات المستقلة |
|
لا يوفر فقط مقياسًا لمدى ملاءمة التنبؤ (حجم المعامل) ، ولكن أيضًا إتجاه معامل إرتباطه (إيجابي أو سلبي) |
يمكن استخدامه فقط للتنبؤ بالدوال غير المترابطة. ومن ثم ، فإن المتغير التابع للانحدار اللوجستي مرتبط بمجموعة الأرقام المنفصلة. |
| سريع جدًا في تصنيف السجلات غير المعروفة. |
لا يمكن حل المسائل غير الخطية باستخدام الانحدار اللوجستي. و نادرًا ما توجد البيانات القابلة للفصل خطيًا في السيناريوهات الواقعية في الحياة اليومية |
|
ذو كفاءة جيدة في التعامل مع البيانات البسيطة و يعمل بشكل جيد أيضا عندما تكون مجموعة البيانات قابلة للفصل بشكل خطي. |
يتطلب الانحدار اللوجستي عدم وجود علاقة خطية متعددة بين المتغيرات المستقلة. |
| يمكنه تفسير معاملات النموذج كمؤشرات لأهمية الميزة. |
من الصعب الحصول على علاقات معقدة باستخدام الانحدار اللوجستي. يمكن للخوارزميات الأكثر قوة و صغرًا مثل الشبكات العصبية أن تتفوق بسهولة على هذه الخوارزمية. |
| الانحدار اللوجستي لا يميل إلى الإفراط في الملاءمة التخصيص، ولكنه قد يزيد من الملاءمة في مجموعات البيانات ذو الأبعاد المتعددة، و لتفادي الإفراط في التخصيص يمكن إستخدام تقنيات الضبط (L1 و L2). |
في الانحدار الخطي ، ترتبط المتغيرات المستقلة والتابعة بشكل خطي. لكن في الانحدار اللوجستي يحتاج إلى أن تكون المتغيرات المستقلة مرتبطة خطيًا ب لوغاريتم الاحتمالات |
التطبيق العملي لخوارزمية الإنحدار اللوجستي سنناقشه في المقال التالي.
المراجع
1- المرجع الاول