تعتبر خوارزمية Naive Bayes من أهم خوارزميات التعلم الالى المتستخدمة في مهام التصنيف. هذه الخوارزمية تعتمد على نظرية بايز مع فرض الاستقلال بين المتغيرات. بعبارة أخرى ، تفترض خوارمية Naive Bayes أن وجود ميزة معينة في فئة لا علاقة لها بوجود أي ميزة أخرى. بمعنى اخر ، تقوم الخوارزمية بعمل التنبؤات من خلال حساب احتمال أن تنتمي نقطة بيانات جديدة إلى فئة معينة بناءً على احتمالية الميزات المرتبطة بهذه الفئة. تفترض الخوارزمية أن الميزات مستقلة عن بعضها البعض ، ولهذا يطلق عليها اسم “ساذج Naive”.
على سبيل المثال ، يمكن للخوارزمية تصنيف الفاكهة على أنها تفاحة إذا كانت حمراء ودائرية وقطرها حوالي 3 بوصات. حتى إذا كانت هذه الميزات تعتمد على بعضها البعض أو على وجود ميزات أخرى ، فإن مصنف Naive Bayes سوف يأخذ بعين الاعتبار كل هذه الخصائص للمساهمة بشكل مستقل في تنبؤ احتمال أن تكون هذه الفاكهة تفاحة.
تتمثل المزايا الرئيسية لـ Naive Bayes في بساطتها وسرعتها ودقتها ، خاصة بالنسبة لمهام تصنيف النص أيضا لمجموعات البيانات الكبيرة جدًا. كما أنها أقل عرضة للإفراط في التخصيص من خوارزميات التعلم الآلي الأخرى. ومع ذلك ، قد لا تعمل مثل الخوارزميات الأخرى الأكثر تعقيدًا عندما تكون البيانات شديدة الارتباط أو عندما يكون هناك عدد كبير من الميزات.
توفر نظرية Bayes طريقة لحساب الاحتمال اللاحق P (c | x) من P (c) و P (x) و P (x | c). انظر إلى المعادلة أدناه:

حيث
P(c | x) هو الاحتمال اللاحق للفئة. P(c) هو الاحتمال السابق للفئة. P(x | c) هو الاحتمال وهو احتمال توقع فئة معينة. P(x) هو الاحتمال السابق للتنبؤ.
طريقة عمل الخوارزمية
لفهم طريقة عمل هذه الخوارزمية لنرى المثال التالي. المثال هو تقدير في ما اذا كانت احتمالية للعب (كرة القدم مثلا) بناءا على احوال الطقس.
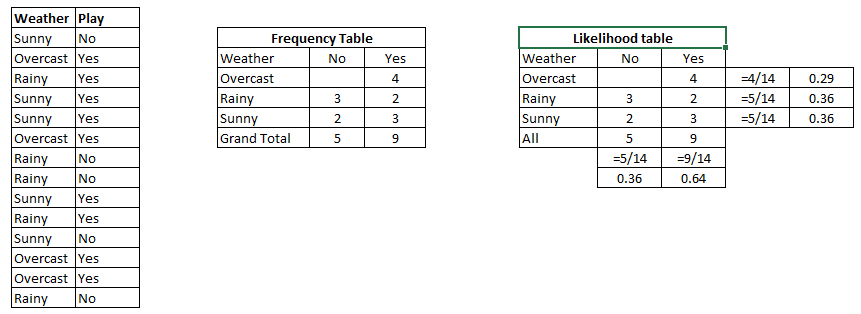
أدناه لدينا مجموعة بيانات تدريبية للطقس ومتغير الهدف المقابل “يلعب” و الاجابة بنعم أو لا. الآن ، نحتاج إلى تصنيف ما إذا كان اللاعبون سيلعبون أم لا بناءً على حالة الطقس. دعنا نتبع الخطوات التالية لتنفيذها.
الخطوة 1: نقوم بتحويل مجموعة البيانات إلى جدول تكراري.
الخطوة 2: نقوم بإنشاء جدول الاحتمالية. من خلال إيجاد الاحتمالات مثلا احتمال ان يكون الجوء غائم = 0.29 واحتمال إمكانية اللعب = 0.64.
الخطوة 3: نقوم بإستخدم معادلة Naive Bayesian لحساب الاحتمال اللاحق لكل فئة. الفئة ذات القيمة الأعلى ل الاحتمال اللاحق هي نتيجة التنبؤ.
المسألة: اللاعبون سيلعبون إذا كان الطقس مشمسًا ، هل هذه العبارة صحيحة؟
يمكننا حلها باستخدام الطريقة التي تمت مناقشتها أعلاه ، لذلك ف
P(Yes | Sunny) = P(Sunny | Yes) * P(Yes) / P (Sunny)
هنا لدينا
P (Sunny |Yes) = 3/9 = 0.33
P(Sunny) = 5/14 = 0.36
P(Yes)= 9/14 = 0.64
اذن
P (Yes | Sunny) = 0.33 * 0.64 / 0.36 = 0.60
القيمة 0.6 هي قيمة احتمال ذو قيمة نوعا ما عالية.
تستخدم خوارزمية Naive Bayes طريقة مماثلة للتنبؤ باحتمالية فئة مختلفة بناءً على سمات مختلفة. تُستخدم هذه الخوارزمية في الغالب في تصنيف النص ومع مسائل وجود فئات متعددة.
أنواع خوارزمية Naive Bayes
هناك أنواع مختلفة من خوارزمية Naive Bayes ، ولكن أكثرها شيوعًا هي مصنفات Gaussian Naive Bayes و Multinomial Naive Bayes و Bernoulli Naive Bayes. حيث يعتمد اختيار المصنف بناءا على نوع البيانات التي يتم تحليلها والافتراضات التي يمكن إجراؤها حول البيانات.
مصنف (GNB) Gaussian Naive Bayes
المصنف Gaussian Naive Bayes يفترض أن الميزات مستمرة وموزعة بشكل طبيعي. يتم استخدامه بشكل شائع لمشاكل التصنيف حيث يكون للميزات توزيع غاوسي أو طبيعي، كما هو الحال في معالجة اللغة الطبيعية ، حيث قد تمثل الميزات عدد الكلمات أو الترددات.
مصنف (MNB) Multinomial Naive Bayes
يتم استخدام مصنف Multinomial Naive Bayes لبيانات العد المنفصلة ، مثل عدد الكلمات في تصنيف النص. يفترض أن الميزات مستقلة وتتبع توزيعًا متعدد الحدود. يتم استخدامه بشكل شائع لتصنيف المستندات ، وتصفية البريد العشوائي ، وتحليل المشاعر.
مصنف (CNB) Complement Naive Bayes
مصنف Complement Naive Bayes هو تطوير لخوارزمية Multinomial Naive Bayes القياسية التي تم تصميمها لمعالجة مشكلة مجموعات البيانات غير المتوازنة. في Multinomial Naive Bayes التقليدية ، تقدر الخوارزمية تكرار كل ميزة في كل فئة ، مما قد يؤدي إلى نتائج متحيزة إذا كانت مجموعة البيانات غير متوازنة. في CNB ، تقدر الخوارزمية تكرار كل ميزة في تكملة كل فئة ، مما يقلل من تأثير الفئة المهيمنة ويمكن أن يؤدي إلى أداء أفضل على مجموعات البيانات غير المتوازنة.
مصنف (BNB) Bernoulli Naive Bayes
مصنف (CNB) Categorical Naive Bayes
مصنف Categorical Naive Bayes هو مصنف متعدد الحدود مصمم للبيانات الفئوية. يفترض أن كل ميزة يمكن أن تأخذ واحدة من مجموعة محدودة من الفئات وتخصص احتمالية لكل فئة بناءً على تكرار الفئة في كل فئة. يتم استخدام CatNB بشكل شائع في مهام تصنيف النص حيث تكون الميزات فئوية ، مثل تصنيف الموضوعات أو تحليل المشاعر.
مثال عملي لمصنف Naive Bayes
هذا كود خوازمية مصنف Gaussian Naive Bayes في بايثون لتصنيف زهرة Iris
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# load the iris dataset
iris = load_iris()
# split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=0)
# create a Gaussian Naive Bayes classifier
clf = GaussianNB()
# train the classifier using the training data
clf.fit(X_train, y_train)
# make predictions on the test data
y_pred = clf.predict(X_test)
# evaluate the performance of the classifier
from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_test, y_pred)
print('Accuracy:', accuracy)
يمكن تشغيل الكود على Colab بالضغط هنا