خوارزمية أقرب الجيران kNN
تعتبر خوارزمية أقرب الجيران من إحدى أهم وأبسط خوارزميات التعليم الالي الخاضع للإشراف. كما أن خوارزمية أقرب الجيران من خوارزميات التي تستخدم في مهام التصنيف و التنبوء. لها القدرة أيضا على التعامل مع البيانات الشاذة أو القيم المتطرفة بكفاءة عالية. الفكرة الأساسية وراء خوارزمية kNN هي تحديد الصنف أو قيمة عينة جديدة بناءً على موقعها من أقرب عينات من مجموعة بيانات التدريب.
كيف تعمل خوارزمية أقرب الجيران kNN
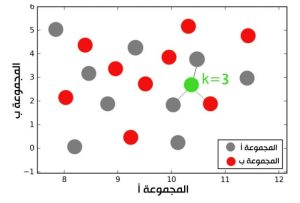
يعتمد مبدأ عمل هذه الخوارزمية على حساب المسافة الاقليدية بين النقاط ، حيث كلما قلت المسافة بين نقطتين زادت إحتمالية إنتماء النقطتين بعضهما لبعض و من هنا جاء إسم الخوارزمية ، و يشير الحرف k إلى عدد العينات التي سيتم تصنيف نقطة ما بناء على المسافات بينها و بين جيرانها الذين يبلغ عددهم k. يعني إذا افترضنا أن k = 3 فإن الخوارزمية تقيس المسافة بين النقطة المستهدفة و أقرب ثلاث نقاط إليها فإذا كانت أقرب نقطتين تنتمي للمجموعة أ والنقطة الثالثة لوحدها تنتمي للمجموعة ب فإن النقطة المستهدفة سيتم تصنيفها على أساس أنها تنتمي للمجموعة أ. كما في الصورة أدناه شكل 2-2.
شكل 2. مبدأ عمل خوارزمية أقرب الجيران
فيما يلي شرح خطوة بخطوة لكيفية عمل خوارزمية kNN رياضيًا:
المعالجة المسبقة
- قم بإعداد مجموعة بيانات التدريب عن طريق تحويل البيانات إلى تنسيق مناسب ، مثل المصفوفة أو إطار البيانات ، والتي يمكن معالجتها بسهولة بواسطة خوارزمية kNN.
- قم بتسوية الخصائص ، إذا لزم الأمر ، للتأكد من أن كل خاصية لها نفس المقياس.
- قسّم البيانات إلى مجموعتين مجموعة تدريب ومجموعة اختبار لتقييم أداء الخوارزمية.
حساب المسافة
لكل عينة في مجموعة التدريب، احسب المسافة بين كل عينة و عينة في مجموعة بيانات التدريب باستخدام مقياس مسافة مناسب ، مثل المسافة الإقليدية أو مسافة مانهاتن.
ابحث عن أقرب الجيران
قم بفرز المسافات بترتيب تصاعدي وحدد K الأقرب جيرانًا استنادًا إلى قيمة K ، وهي معلمة تحددها أنت.
تحديد الفئة أو القيمة
بالنسبة لمسائل التصنيف ، حدد فئة العينة الجديدة بناءً على فئة الأغلبية لأقرب جيران K. إذا كانت الأصناف متوازنة ، فسيتم اختيار الصنف الذي يتمتع بأغلبية الأصوات.
بالنسبة لمسائل التنبؤ ، حدد قيمة العينة الجديدة بناءً على متوسط قيمة أقرب جيران K.
تقييم الأداء
قم بتقييم أداء الخوارزمية من خلال مقارنة الفئة أو القيمة المتوقعة للعينة الجديدة بالفئة أو القيمة الفعلية.
كرر الخطوات من الثانية إلى الخامسة لجميع العينات في مجموعة الاختبار واحسب الدقة أو مقاييس الأداء الأخرى لتقييم الأداء العام للخوارزمية. هذا هو التفسير الرياضي الأساسي لكيفية عمل خوارزمية أقرب الجيران. من الناحية العملية ، هناك العديد من التعديلات في خوارزمية kNN التي تم تطويرها للتغلب على قيود معينة ، مثل الأبعاد ، واختيار قياس المسافة ، أو وقت الحساب.
بناء الخوارزمية رياضيا و من الصفر في بايثون
import numpy as np
import operator
class KNN:
def __init__(self, k):
self.k = k
def fit(self, X, y):
self.X_train = X
self.y_train = y
def predict(self, X):
y_pred = []
for sample in X:
distances = [np.linalg.norm(sample - x) for x in self.X_train]
closest_samples = np.argsort(distances)[:self.k]
closest_labels = [self.y_train[i] for i in closest_samples]
most_common_label = max(set(closest_labels), key=closest_labels.count)
y_pred.append(most_common_label)
return y_pred
# example usage
X_train = np.array([[1, 2], [2, 4], [4, 6], [5, 7]])
y_train = np.array([0, 1, 1, 1])
X_test = np.array([[3, 5], [5, 8]])
knn = KNN(3)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
print(y_pred)
الأشياء التي يجب مراعاتها قبل اختيار خوارزمية أقرب الجيران
- تعتبر هذه الخوارزمية مكلفة حسابيا
- يجب أن تكون المتغيرات مسواة ، وإلا فإن متغيرات النطاق الأعلى يمكن أن تتحيز لفئة معينة
- يحبذ معالجة البيانات قبل تطبيق الخوارزمية عليها مثل إزالة القيم المتطرفة.
مميزات خوارزمية أقرب الجيران
- لا تتضمن على عملية تدريب للبيانات, البيانات نفسها هي نموذج ستكون مرجعًا للتنبؤ المستقبلي و لهذا السبب فهي فعالة للغاية من حيث الوقت و من حيث الارتجال للنمذجة العشوائية على البيانات المتاحة.
- تعتبر خوارزمية الجار الأقرب سهلة التنفيذ للغاية حيث أن الشيء الوحيد الذي يجب حسابه هو فقط المسافة بين النقاط المختلفة على أساس بيانات الميزات المختلفة ويمكن بسهولة حساب هذه المسافة باستخدام دالة المسافة سواء الإقليدية Euclidean أو مانهاتن Manhattan.
- نظرًا لعدم وجود عملية تدريب للبيانات يمكن إضافة بيانات جديدة في أي وقت لأنها لن تؤثر على أداء النموذج.
عيوب خوارزمية أقرب الجيران
- لا تعمل بشكل جيد مع مجموعة البيانات الكبيرة لأن حساب المسافات بين كل عينة للبيانات سيكون مكلفًا للغاية.
- لا تعمل بشكل جيد مع البيانات ذات الأبعاد المتعددة لأن هذا سيعقد عملية حساب المسافة لكل بُعد.
- حساسة جدا للبيانات المتطرفة أو المفقودة.