يعتبر كل من الانحدار الخطي والانحدار اللوجستي من أهم خوارزميات التعلم الآلي التي تعد جزءًا من نماذج التعلم الخاضع للإشراف. و نظرًا لكونهما جزء من نماذج التعلم الآلي الخاضع للإشراف ، لذا فهما يستفيدان من البيانات الموسومة labeled data لإجراء التنبؤات.

يستخدم الانحدار الخطي للتنبؤ بالقيم المستمرة بينما يمكن استخدام الانحدار اللوجستي في للتنبؤ بالقيم الفئوية والمستمرة على حد سواء ، ولكنه يستخدم على نطاق واسع كخوارزمية تصنيف. تهدف نماذج الانحدار إلى توقع القيمة بناءً على ميزات مستقلة.

الاختلاف الرئيسي الذي يجعل كلاهما مختلفين عن بعضهما البعض هو عندما تكون المتغيرات التابعة ثنائية أو ثلاثية بمعنى أخر فئوية فعندئذ يتم إستخدام الانحدار اللوجستي أما عندما تكون المتغيرات التابعة مستمرة ،عندئذ يتم استخدام الانحدار الخطي.

الانحدار الخطي

الانحدار الخطي هو نفس النموذج المستخدم على نطاق واسع في التحليل التنبئي Predictive analysis. هذا النموذج يوضح لنا بشكل رئيسي عن العلاقة بين الهدف target – متغير تابع dependent variable – والميزات predictors باستخدام خط مستقيم. الانحدار الخطي قد يكون انحدار خطي بسيط و انحدار خطي متعدد. بحيث أن الانحدار الخطي البسيط يحتوي على متغير مستقل واحد فقط بينما الانحدار المتعدد يمكن أن يكون هناك أكثر من متغير مستقل واحد.

لنفهم طريقة عمل النوذج هذا دعونا نطبق مسألة من مسائل الإنحدار. سنستخدم في هذا المثال مجموعة بيانات بوسطن  Boston dataset من مكتبة Scikit-Learn ، تحتوي مجموعة البيانات هذه على معلومات حول قيمة المنزل لمنازل مختلفة في مدينة بوسطن. المتغيرات الأخرى الموجودة في مجموعة البيانات هذه هي معدل الجريمة ، مناطق الأعمال غير التجارية في المدينة (INDUS) ، بالإضافة إلى متغيرات أخرى.

أولا سنقوم باستيراد جميع المكتبات المهمة والأهم من ذلك ، استيراد مجموعة البيانات من مكتبة sklearn.datasets.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
boston = load_boston()
boston.data.shape, boston.target.shape
>> output   ((506, 13), (506,))

ثانيا سنقوم بعرض مجموعة البيانات بيانيا بمساعدة مكتبة pandas ، وسنقوم بتسمية ميزات مجموعة البيانات وبعد ذلك ، سنقوم بإنشاء إطار بيانات بإستخدام مكتبة pandas.

boston.feature_names
bos = pd.DataFrame(boston.data)
bos.columns = boston.feature_names
print(bos.head())
>> output 
  CRIM    ZN   INDUS CHAS NOX   ... RAD TAX   PTRATIO B L    STAT 
0 0.00632 18.0 2.310 0.00 0.538 ... 1.0 296.0 15.3    396.90 4.98 
1 0.02731 0.00 7.070 0.00 0.469 ... 2.0 242.0 17.8    396.90 9.14 
2 0.02729 0.00 7.070 0.00 0.469 ... 2.0 242.0 17.8    392.83 4.03 
3 0.03237 0.00 2.180 0.00 0.458 ... 3.0 222.0 18.7    394.63 2.94 
4 0.06905 0.00 2.180 0.00 0.458 ... 3.0 222.0 18.7    396.90 5.33 

[5 rows x 13 columns]

ثالثا في هذه الخطوة ، سنقسم مجموعة البيانات إلى مجموعة تدريب و مجموعة اختبار.

X_train, X_test, y_train, y_test = train_test_split(boston.data, 
                                    boston.target, test_size=0.2)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
>> output (404, 13) (102, 13) (404,) (102,)

رابعا نقوم بملائمة مجموعة البيانات الخاصة بنا مع نموذج التعلم الآلي من sklearn لتنفيذ الانحدار الخطي.

sklinreg = LinearRegression(normalize=True)
sklinreg.fit(X_train, y_train)
>> output LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=True)

أخيرا ، نقوم بإختبار نتائج التدريب و الاختبار على مجموعة البيانات الخاصة بنا.

print("Train:", sklinreg.score(X_train, y_train))
print("Test:", sklinreg.score(X_test, y_test))
>> output Train: 0.7221378898881832 
          Test: 0.8065460951660129

الانحدار اللوجستي

خوارزمية يتم استخدامها على نطاق واسع في مهام التصنيف. يتم استخدامه للتنبؤ بالمتغيرات الفئوية بمساعدة المتغيرات التابعة. ضع في اعتبارك أن هناك فئتين ونقطة بيانات جديدة يجب التحقق من الفئة التي تنتمي إليها. ثم تحسب الخوارزميات قيم الاحتمالات التي تتراوح ما بين 0 و 1. على سبيل المثال ، هل ستمطر اليوم أم لا. في الانحدار اللوجستي ، يتم تمرير مجموع المدخلات المرجح من خلال sigmoid activation function ويسمى المنحنى الذي يتم الحصول عليه بمنحنى سيقمويد sigmoid curve. الدالة اللوجيستية التي هي دالة سيقمويد هي منحنى على شكل حرف “S” يأخذ أي قيم حقيقية ويحولها إلى 0 أو 1. إذا كان الناتج المعطاه من دالة سيقمويد أكثر من 0.5 ، فسيتم تصنيف الناتج على أنه 1 وإذا كان أقل من 0.5 ، فسيتم تصنيف الناتج على أنه 0. إذا وصل الرسم البياني إلى سالب مالا نهاية ، فإن y المتوقع سيكون 0 والعكس صحيح .

لفهم الإنحدار اللوجستي أكثر دعونا نرى المثال التالي على بيانات عشوائية سيتم إنشائها ضمن الخطوات التالية:

أولا سنقوم باستيراد جميع المكتبات المهمة

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression as SKLR

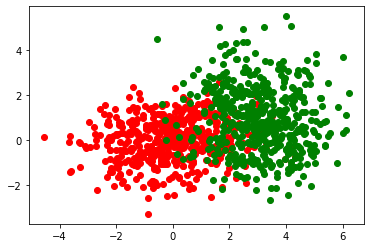
ثانيا نقوم بإنشاء مجموعة بيانات مكونة من 1000 صف وعمودين و نقوم برسم مجموعة البيانات هذه بمساعدة مكتبة matplotlib.

mean_01 = [0,0]
cov_01 = [[2,0.2], [0.2,1]]
mean_02 = [3,1]
cov_02 = [[1.5,-0.2], [-0.2,2]]
dist_01 = np.random.multivariate_normal(mean_01, cov_01, 500)
dist_02 = np.random.multivariate_normal(mean_02, cov_02, 500)
print(dist_01.shape, dist_02.shape)
>> output (500, 2) (500, 2)

plt.figure()
plt.scatter(dist_01[:,0], dist_01[:,1], color='red')
plt.scatter(dist_02[:,0], dist_02[:,1], color='green')
plt.show()
>> output

ثالثا عند إضافة كلا التوزيعين ، تتم إضافة “1” هنا بسبب عمود التسمية

يتم توزيع أول 500 نقطة بيانات للتوزيع الأول

أيضا يتم توزيع فيما بعد 500 نقطة بيانات للتوزيع الثاني

و عمل عمود منفصل للتسميات.

dataset = np.zeros((dist_01.shape[0] + dist_02.shape[0], dist_01.shape[1] + 1))
dataset[:dist_01.shape[0], :-1] = dist_01
dataset[dist_01.shape[0]:, :-1] = dist_02
 # Red = 0, Green = 1
 dataset[dist_02.shape[0]:, -1] = 1
dataset.shape
>> Output (1000, 3)

لاحقا يتم تبديل مجموعة البيانات عشوائيًا بحيث يتم خلط التوزيعين بشكل صحيح بحيث يعملان كمجموعة بيانات حقيقية ومن ثم يتم تقسيم مجموعة البيانات لمجموعة تدريب ومجموعة اختبار ثم نرسم الشكل البياني لمجموعة البيانات

np.random.shuffle(dataset)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(dataset[:,:-1], dataset[:,-1], test_size=0.2)
X_train.shape, X_test.shape, y_train.shape, y_test.shape
>> Output ((800, 2), (200, 2), (800,), (200,))

أخيرا نقوم بملائمة البيانات على نموذج الإنحدار اللوجستي

sk_logreg = SKLR()
sk_logreg.fit(X_train, y_train)
>> Output LogisticRegression(C=1.0, class_weight=None, dual=False, 
                fit_intercept=True, intercept_scaling=1, l1_ratio=None, 
                max_iter=100, multi_class='auto', n_jobs=None, penalty='l2', 
                random_state=None, solver='lbfgs', tol=0.0001, verbose=0, 
                warm_start=False)

sk_logreg.score(X_test, y_test)
>> Output 0.89

لقد أختبرنا النموذج و حصلنا على دقة تساوي 89%.

المراجع

1- المرجع الأول

2- المرجع الثاني