الإنحدار الخطي Linear regression

تحدثنا في الباب السابق عن أنواع تعلم الآلة وذكرنا أن من بينها التعلم الخاضع للاشراف وهو النوع الذي يتعلم من بيانات تدريبية. و ذكرنا أن هناك نوعين من المهام مهام التصنيف و مهام التنبؤ.  نتحدث هنا في هذا المقال عن الانحدار الخطي Linear regression و كيفية استخدامه في استخراج وتحديد العلاقات من البيانات والاستفادة من هذه العلاقات في مهام التنبوء.

تعريف الإنحدار الخطي

الانحدار الخطي هو خوارزمية إحصائية تستخدم لنمذجة العلاقة بين متغيرين. تفترض هذه الخوارزمية أن هناك علاقة خطية بين المتغير التابع (المتغير الذي يتم توقعه أو شرحه) و متغير واحد أو أكثر من المتغيرات المستقلة (تلك المستخدمة لإجراء التنبؤ). الهدف من الانحدار الخطي هو العثور على الخط الأنسب الذي يصف العلاقة بين المتغيرات. حيث يتم تحديد أفضل خط مناسب بتقليل مجموع الفروق التربيعية بين القيم الفعلية والقيم المتوقعة.

الانحدار الخطي نوعان: الانحدار الخطي البسيط و الانحدار الخطي المتعدد. يتميز الانحدار الخطي البسيط بمتغير مستقل واحد. بينما يتميز الانحدار الخطي المتعدد بالعديد من المتغيرات المستقلة (أكثر من واحد) أثناء البحث عن أفضل خط مناسب.  يمكن تمثيل الانحدار البسيط بالمعادلة ادناه:

y = bX + c

حيث: y متغير تابع , b –  الميل , X  متغير مستقل , c تقاطع.

بينما يتم تمثيل الانحدار متعدد المتغيرات بالمعادلة أدناه:

 y = b₁x₁ + b₂x₂ + … + b_nx_n + c

حيث: y متغير تابع , b₁  ميل المتغير 1, b₂  ميل المتغير 2, b_n  متغير مستقل رقم (n), x₁  متغير مستقل رقم 1, x₂  متغير مستقل رقم 2, x_n  متغير مستقل رقم (n), c تقاطع.

الانحدار الخطي البسيط

لايجاد العلاقة بين متغيرين احدهما مستقل والأخر تابع (يتغير بتغير المستقل). وكلمة خطي جاءت من كون العلاقة تكون في شكل خط مستقيم (تذكر معادلة الخط المستقيم ). ويمكننا تكوين نموذج رياضي لتمثيل هذه العلاقة. الانحدار الخطي البسيط هو دراسة العلاقة بين متغيرين فقط بحيث نحاول الوصول الى علاقة خطية (أي معادلة خط مستقيم ) بين هذين المتغيرين ، مثل العلاقة بين السعر والسلعة او بين درجة الحرارة وإستهلاك الكهرباء.

في الانحدار الخطي البسيط يمكننا التنبوء بقيم متغير معين (التابع) بناءا على قيم متغير ثاني (المستقل)

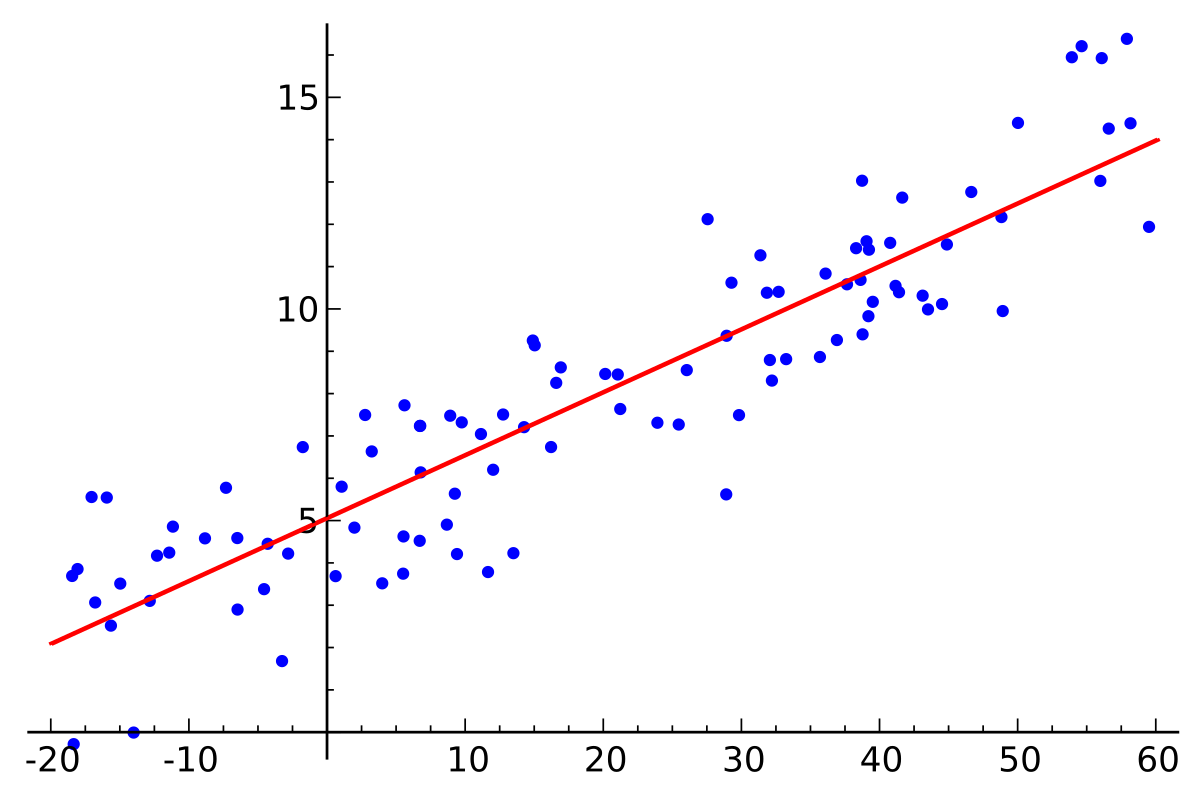
الغرض الأساسي من الانحدار هو العثور على أفضل خط مستقيم يمر خلال النقاط مع اقل نسبة خطأ. في الشكل أعلاه يسمى الخط الظاهر باللون الأحمر بخط الانحدار ويتكون من النتيجة المتوقعة على Y لكل قيمة ممكنة لـ  X . تمثل الخطوط العمودية من النقاط الى خط الانحدار أخطاء التنبؤ. نلاحظ أن النقطة الزرقاء القريبة من خط الإنحدار يعتبر خطأها في التنبؤ صغير. على النقيض من ذلك ، فان النقطة البعيدة بكثير من خط الإنحدار ، يكون خطأ التنبؤ لديها كبير.

الانحدار متعدد المتغيرات

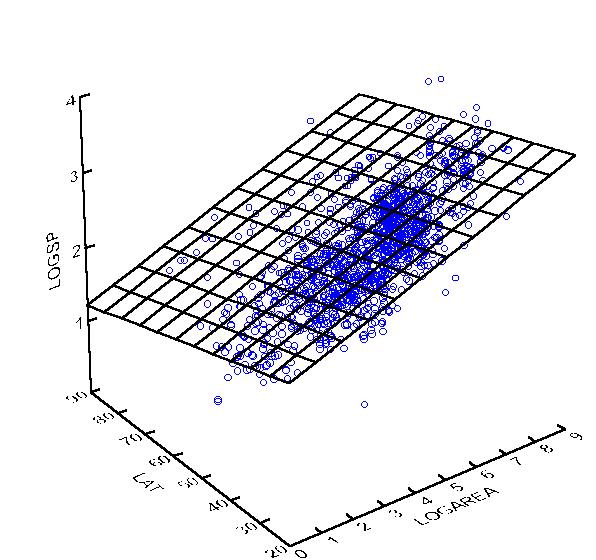
هذا النوع من الانحدار معروف أيضًا باسم الانحدار المتعدد ، هو أسلوب إحصائي يستخدم لتحليل العلاقة بين المتغيرات المستقلة المتعددة والمتغير التابع . الانحدار المتعدد هو امتداد طبيعي للانحدار الخطي البسيط ، والذي يتضمن متغيرًا مستقلاً واحدًا ومتغيرًا تابعًا واحدًا. في هذا النوع من الانحدار ، الهدف هو العثور على أفضل معادلة خطية تشرح العلاقة بين المتغير التابع والعديد من المتغيرات المستقلة في وقت واحد. يتم التعبير عن المعادلة من حيث معاملات الانحدار التي تعكس قوة واتجاه العلاقة بين كل متغير مستقل و المتغير التابع ، مع التحكم في تأثيرات المتغيرات المستقلة الأخرى في النموذج. نموذج هذا الانحدار مفيد للتنبؤ بقيم المتغير التابع بناءً على قيم المتغيرات المستقلة. يمكن استخدامه أيضًا لاختبار الفرضيات حول العلاقة بين المتغيرات المستقلة والمتغير التابع ، وكذلك لتحديد المتغيرات المستقلة التي لها أقوى تأثير على المتغير التابع.

مثال

مثال على ذلك عندنا كشف درجات 105 طالب (يحتوي هذا الكشف على معدل الطالب في الثانوية و معدله في الجامعة) في تخصص علم الحاسب. نريد بناءا على هذه البيانات التنبؤ بمعدل الطالب في الجامعة إعتمادا على معدله السابق بالثانوية. لحل هذا المثال سنستخدم الانحدار ليتعلم من البيانات الموجودة (وهي درجات الطلاب ال 105) من اجل إيجاد معادلة الانحدار التي هي في هذا المثال معادلة خطية حيث تمثل الحل وهي كما يلي:

معدل الطالب بالجامعة = 0.675*معدل الطالب في الثانوية + 1.097

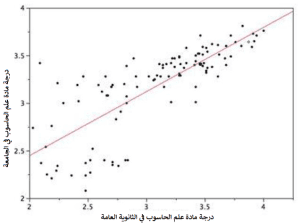
و يمثل الشكل أعلاه الحل، حيث يتضح من الشكل أن هنالك علاقة إيجابية قوية وكان معامل الاتباط 0.675. الوصول لمعامل الارتباط وإيجاد المعادلة التي تمثل العلاقة بين درجات الطلاب هو ما تعلمه الانحدار من البيانات. بعدها سيكون قادرا على التنبوء بمعدل أي طالب في الجامعة إذا ما أعطي معدله بالثانوية. مثلا لو كان لدينا طالب ثانوي حصل على معدل 3 ، فان معدله المتوقع له بالجامعة هو  3.12 ، وذلك بالتعويض في معادلة الحل، كما يلي:  0,675 * 3 + 1,097 = 3,12.