تعتبر خوارزمية مونت كارلو Monte Carlo algorithm تقنية حسابية قوية لها إستخدامات عديدة لحل المشكلات الرياضية المعقدة. حيث سميت هذه الخوارزمية على اسم كازينو مونتي كارلو الشهير في مدينة موناكو ، و الذي يعتبر من أشهر مواقع الجذب السياحي في موناكو. تستخدم هذه الخوارزمية عينات عشوائية لتقدير حل مشكلة ما. لذلك سنشرح في هذا المقال مفهوم الخوارزمية و تطبيقاتها هذا بالاضافة إلى مثال عملي في بايثون لتعلم طريقة عمل الخوارزمية. من ناحية أخرى هذا المقال مرتبط بمقال عن خورازمية الغابة العشوائية.
ما هي خوارزمية مونت كارلو؟
تعتبر هذه الخوارزمية طريقة إحصائية يتم إستخدامها لتقدير حل مشكلة ما عن طريق توليد عينات عشوائية. بمعنى آخر ، إنها تقنية عددية تستخدم الأرقام العشوائية ونظرية الاحتمالات لتقدير حل مشكلة ما.
تطبيقات الخوارزمية
تحتوي خوارزمية مونت كارلو على مجموعة واسعة من التطبيقات في مختلف المجالات مثل المالية والفيزياء والهندسة وعلوم الحاسوب. بعض تطبيقاتها كالتالي:
- المالية: يتم استخدام خوارزمية مونت كارلو لمحاكاة سلوك الأصول المالية مثل الأسهم والسندات. تُستخدم هذه التقنية لتقدير القيمة المستقبلية للاستثمار عن طريق إنشاء سيناريوهات عشوائية للسوق.
- الفيزياء: تُستخدم خوارزمية مونت كارلو لمحاكاة سلوك الجسيمات في نظام ما. تستخدم هذه التقنية لتقدير سلوك الذرات والجزيئات في فيه.
- الهندسة: تُستخدم خوارزمية مونت كارلو لمحاكاة سلوك الأنظمة المعقدة مثل المباني والجسور. تستخدم هذه التقنية لتقدير سلوك الهيكل في ظل ظروف مختلفة مثل الرياح والزلازل.
- علوم الحاسوب: تُستخدم الخوارزمية لتقدير أداء الخوارزميات كذلك تُستخدم هذه لتقدير وقت تشغيل الخوارزمية عن طريق توليد مدخلات عشوائية.
تطبيق عملي للخوارزمية
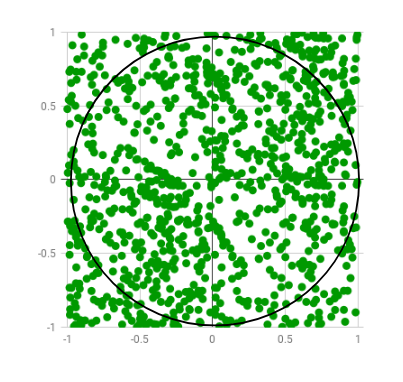
في هذا الجزء ، سنحاول فهم طريقة عمل الخوارزمية بمثال على بايثون. على سبيل المثال ، دعونا ننظر في المثال التالي طريقة تقدير قيمة باي π باستخدام خوارزمية مونت كارلو. الفكرة هي إنشاء نقاط عشوائية داخل مربع طول ضلعه وحدتان ، و رسم دائرة نصف قطرها وحدة و احدة داخل المربع. يجب أن تكون نسبة عدد النقاط داخل الدائرة إلى إجمالي عدد النقاط المتولدة مساوية لنسبة مساحة الدائرة إلى مساحة المربع. بناء على هذه النسبة ، يمكننا تقدير قيمة π بأربعة أضعاف النسبة.
مساحة الدائرة تساوي
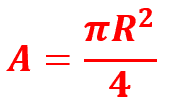
بينما مساحة المربع تساوي
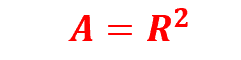
يعني نسبة مساحة الدائرة إلى مساحة المربع تساوي π/4 فمثلا عند رمي النقاط عشويا لو كان عدد النقط المرمية داخل الدائرة تساوي 40 بينما عدد النقاط الكلية تساوي 51 نقطة عندئذ قيمة باي π تساوي (40/51) * 4 تساوي 3,13.
إليك كود البايثون لتطبيق هذه الخوارزمية:
import random
INTERVAL = 1000
circle_points = 0
square_points = 0
# Total Random numbers generated= possible x
# values* possible y values
for i in range(INTERVAL**2):
# Randomly generated x and y values from a
# uniform distribution
# Range of x and y values is -1 to 1
rand_x = random.uniform(-1, 1)
rand_y = random.uniform(-1, 1)
# Distance between (x, y) from the origin
origin_dist = rand_x**2 + rand_y**2
# Checking if (x, y) lies inside the circle
if origin_dist <= 1:
circle_points += 1
square_points += 1
# Estimating value of pi,
# pi= 4*(no. of points generated inside the
# circle)/ (no. of points generated inside the square)
pi = 4 * circle_points / square_points
## print(rand_x, rand_y, circle_points, square_points, "-", pi)
# print("\n")
print("Final Estimation of Pi=", pi)
في هذا الكود ، نحدد دالة “estimate_pi” تأخذ عدد العينات n كمدخلات. داخل الدالة ، نولد عددًا من النقاط العشوائية داخل مربع طول الضلع وحدتين. لكل نقطة ، نتحقق مما إذا كانت تقع داخل دائرة نصف قطرها وحدة واحدة. بناء على ذلك ، إذا كانت النقطة تقع داخل الدائرة ، فإننا نزيد العد. في النهاية ، نعيد القيمة المقدرة لـ pi بمقدار 4 أضعاف نسبة عدد النقاط داخل الدائرة إلى إجمالي عدد النقاط المتولدة.
الخلاصة
تعد خوارزمية مونت كارلو تقنية حسابية قوية تستخدم عينات عشوائية لتقدير حل مشكلة ما. لديها مجموعة واسعة من التطبيقات في مختلف المجالات، على سبيل المثال المالية والفيزياء والهندسة وعلوم الكمبيوتر. علاوة على ذلك ، شرحنا في هذا المقال مفهوم الخوارزمية و تطبيقاتها و قدمنا مثال على إستخدام الخوارزمية على بايثون.