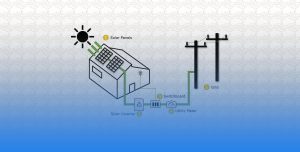
خوازمية شجرة القرار Decision Tree
خوازمية شجرة القرار Decision Tree هي خوارزمية من خوارزميات تعلم الآلة تقوم بتحليل البيانات وتقسيمها إلى فئات (أو تصنيفات) باستخدام سلسلة من القرارات المستندة إلى القيم الموجودة في مجموعة من المتغيرات. ويتم تمثيل هذه القرارات في شكل هيكل شجري، حيث يتم تقسيم البيانات على شكل فروع (Branches) وتصنيفات (Leaves)، ويتم اتخاذ القرارات بناءً على معايير محددة.
تستخدم شجرة القرار في العديد من التطبيقات مثل التصنيف و التنبؤ، حيث يتم استخدامها لتصنيف العناصر إلى فئات مختلفة بناءً على متغيرات معينة. كما يمكن استخدامها في تحليل البيانات واكتشاف العلاقات السببية بين المتغيرات.
تندرج خوارزمية شجرة القرار إلى فئة خوارزميات التعلم تحت الإشراف. على عكس خوارزميات التعلم تحت الإشراف الأخرى ، يمكن استخدام خوارزمية شجرة القرار لحل مشاكل الانحدار والتصنيف أيضًا.
الدافع العام لاستخدام خوارزمية شجرة القرار هو إنشاء نموذج تدريب يمكن استخدامه للتنبؤ بفئة أو قيمة المتغيرات المستهدفة من خلال تعلم قواعد القرار المستنتجة من البيانات السابقة (بيانات التدريب).
خوارزمية أشجار القرار سهلة للغاية مقارنة بخوارزميات التصنيف الأخرى. تحاول خوارزمية شجرة القرار حل المشكلة باستخدام تمثيل الشجرة. تتوافق كل عقدة داخلية للشجرة مع سمة ، وكل عقدة طرفية تتوافق مع تسمية فئة.
طريقة عمل الخوارزمية
تعمل خوارزمية شجرة القرار عن طريق تحليل البيانات واستخراج العلاقات بين المتغيرات المختلفة للوصول إلى قرار تصنيف دقيق. ويتم ذلك بالخطوات التالية:
1- اختيار المتغيرات: يتم اختيار المتغيرات التي تؤثر على النتيجة المرجوة وتستخدم لتصنيف البيانات. ضع أفضل سمة لمجموعة البيانات في جذر الشجرة.
2- قسم مجموعة التدريب إلى مجموعات فرعية . يجب عمل مجموعات فرعية بطريقة تحتوي كل مجموعة فرعية على بيانات بنفس قيمة السمة. تقسيم البيانات: يتم تقسيم البيانات إلى مجموعة صغيرة من الأقسام (subsets) باستخدام المتغيرات المختارة، حيث يتم تحليل القيم المختلفة لكل متغير وتقسيم البيانات إلى فروع مختلفة بناءً على قيمة المتغيرات.
3- حساب الاختلافات: يتم حساب الاختلافات بين فروع البيانات المختلفة، ويتم اختيار الفرع الذي يعطي أفضل تمثيل للبيانات.
4- إنشاء الشجرة: يتم إنشاء شجرة القرار عن طريق تكرار الخطوات السابقة حتى يتم تقسيم البيانات إلى مجموعات فرعية مختلفة، ويتم تمثيل ذلك في شكل شجرة يتكون من فروع وأوراق.
5- التصنيف: يتم استخدام شجرة القرار المنشأة لتصنيف البيانات الجديدة، حيث يتم اتباع الفروع المناسبة في الشجرة وتحديد التصنيف الذي تنتمي إليه البيانات.
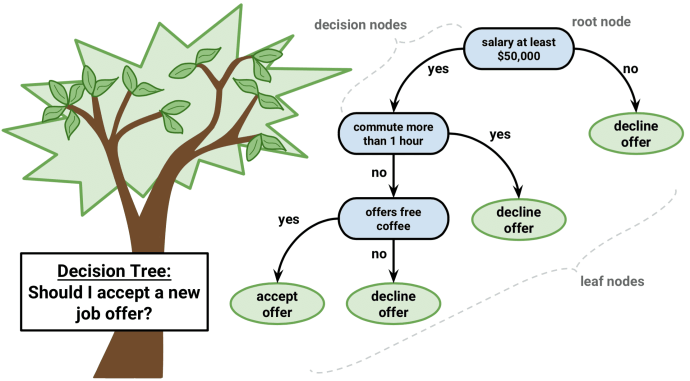
وبما أن عملية إنشاء شجرة القرار تستند إلى التحليل الإحصائي والقواعد المنطقية، فإنها تعد واحدة من أكثر الأدوات شيوعًا في تحليل البيانات وتصنيفها في مختلف المجالات.
في أشجار القرار ، من أجل التنبؤ بمتغير أي فئة لسجل ما نبدأ من جذر الشجرة. نقارن قيم سمة الجذر بسمة السجل. على أساس المقارنة ، نتبع الفرع المقابل لتلك القيمة وننتقل إلى العقدة التالية.
نواصل مقارنة قيم سمات السجل مع العقد الداخلية الأخرى للشجرة حتى نصل إلى عقدة طرفية مع قيمة فئة متوقعة. كما نعلم كيف يمكن استخدام شجرة القرار النموذجية للتنبؤ بالفئة المستهدفة أو القيمة المستهدفة. الآن دعونا نفهم كيف يمكننا إنشاء نموذج شجرة القرار.
الافتراضات في خوازمية شجرة القرار Decision Tree
الافتراضات أثناء إنشاء شجرة القرار. فيما يلي بعض الافتراضات التي نقوم بها أثناء استخدام شجرة القرار:
في البداية ، تعتبر مجموعة التدريب بأكملها هي الجذر. حيث يُفضل أن تكون قيم السمات مقسمه إلى فئات. إذا كانت القيم مستمرة ، فسيتم تقديرها قبل إنشاء النموذج.
يتم توزيع السجلات بشكل متكرر على أساس قيم السمات. حيث يتم ترتيب وضع السمات كجذر أو عقدة داخلية للشجرة باستخدام بعض أدوات النهج الإحصائي.
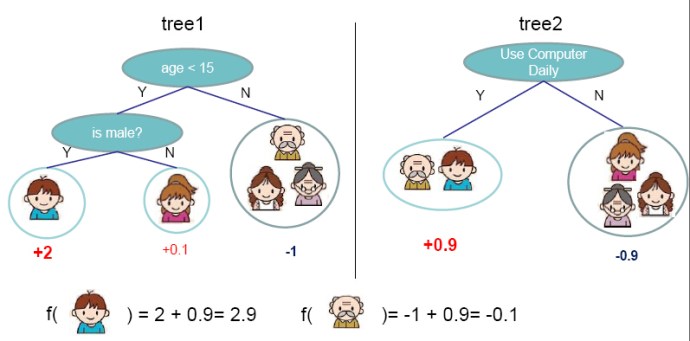
تتبع أشجار القرار مجموع النتائج. بالنسبة للصور أعلاه ، يمكنك أن ترى كيف يمكننا أن نتوقع هل يمكننا قبول عرض العمل الجديد؟ واستخدام الكمبيوتر يوميا؟ من اجتياز العقدة الجذرية إلى العقدة الورقية.
إن تمثيل مجموع النتائج. يُعرف مجموع النتائج أيضًا بالصيغة العادية المنفصلة. بالنسبة للفئة ، فإن كل فرع من جذر الشجرة إلى عقدة الورقة التي لها نفس الفئة هو اقتران (مجموع) للقيم ، تشكل الفروع المختلفة التي تنتهي في تلك الفئة فصلًا (مجموع).
يتمثل التحدي الأساسي في تنفيذ شجرة القرار في تحديد السمات التي نحتاج إلى اعتبارها عقدة الجذر وكل مستوى. معالجة هذا هو معرفة اختيار السمات. لدينا مقياس اختيار سمات مختلف لتحديد السمة التي يمكن اعتبارها ملاحظة الجذر في كل مستوى. مقاييس اختيار السمة الافضل هي Information gain و Gini index.
مشكلة الافراط في التخصيص في الخوارزمية
تعد مشكلة الافراط في التخصيص مشكلة من المشاكل التي يتم مواجهتها أثناء بناء نموذج شجرة القرار. النموذج يواجه مشكلة الافراط في التخصيص عندما تستمر الخوارزمية في التعمق أكثر في تقليل أخطاء مجموعة التدريب ولكن ينتج عنها زيادة في خطأ مجموعة الاختبار ، أي تنخفض دقة التنبؤ لنموذجنا. يحدث هذا بشكل عام عندما يبني العديد من الفروع بسبب القيم الخطأ في البيانات.
هناك طريقتان يمكننا استخدامهما لتجنب الافراط في التخصيص هما:
- مرحلة قبل التقليم Pre-Pruning
في مرحلة قبل التقليم Pre-Pruning ، فإنه يوقف بت بناء الشجرة في وقت مبكر. يفضل عدم تقسيم العقدة إذا كان مقياس الايجابية أقل من قيمة العتبة. ولكن من الصعب اختيار نقطة توقف مناسبة.
- مرحلة بعد التقليم Post-Pruning
في مرحلة بعد التقليم Post-Pruning أولاً ، يكون التعمق أكثر وأكثر في الشجرة لبناء شجرة كاملة. إذا أظهرت الشجرة مشكلة الافراط في التناسب overfitting problem ، فسيتم التقليم Pruning كخطوة Post-Pruning. نستخدم بيانات التحقق cross-validation data المتبادل للتحقق من تأثير التقليم Pruning . باستخدام بيانات التحقق المتبادل cross-validation data، فإنه يختبر ما إذا كان توسيع العقدة سيؤدي إلى تحسين النموذج أم لا.
إذا أظهر تحسنًا ، فيمكننا الاستمرار بتوسيع هذه العقدة. ولكن إذا أظهرت انخفاضًا في الدقة ، فلا يجب توسيعها ، أي يجب تحويل العقدة إلى عقدة طرفية.
مزايا و سلبيات خوازمية شجرة القرار Decision Tree
المزايا:
- من السهل شرح خوارزمية شجرة القرار. ينتج عنه مجموعة من القواعد.
- يتبع نفس النهج الذي يتبعه البشر بشكل عام أثناء اتخاذ القرارات.
- يمكن تبسيط تفسير نموذج شجرة القرار المعقد من خلال تصوره.
- عدد المعلمات الفائقة hyper-parameters المراد ضبطها تكاد تكون خاليًا.
السلبيات:
- هناك احتمال كبير لظهور مشاكل الفرط في التناسب Overfitting في خوارزمية شجرة القرار.
- خوارزمية شجرة القرار بشكل عام ، تعطي دقة تنبؤ منخفضة لمجموعة بيانات مقارنة بخوارزميات التعلم الآلي الأخرى.
- يعطي Information gain في شجرة القرار ذات المتغيرات الفئوية استجابة متحيزة للسمات ذات العدد الأكبر من الفئات.
- يمكن أن تصبح الحسابات معقدة عندما يكون هناك العديد من تصنيفات الفئة class labels.
المراجع