تعتبر خوارزمية K-Means من خوارزميات التعلم غير الخاضع للإشراف و التي تستخدم لحل مهام التصنيف على شكل عناقيد. مبدأ عمل هذه الخوارزمية تتبع طريقة بسيطة وسهلة لتصنيف مجموعة بيانات معينة من خلال عدد معين من العناقيد (مع افتراض أن k عدد العناقيد). مجموعة البيانات داخل العنقودة الواحدة متجانسة لكنها غير متجانسة مع مجموعة البيانات داخل العناقيد الأخرى.
كيف تعمل خوارزمية K-Means على تشكيل العناقيد
- تختار خوارزمية K-Means عدد من النقاط k لكل عنقودة cluster و تعرف باسم النقاط الوسطى centroids.
- تشكل كل نقطة بيانات عنقودة بها النقاط الوسطى القريبة لها، أي k عناقيد.
- إيجاد النقطه الوسطى centroid لكل عنقودة يعتمد على أعضاء العنقودة الحاليين. هنا يظهر لدينا نقاط وسطى جديدة.
- عند ظهور نقاط وسطى جديدة ، تعمل K-Means على تكرار الخطوتين 2 و 3. بحيث تبحث عن أقرب مسافة لكل نقطة بيانات من النقاط الوسطى الجديدة وتعمل على ربطها ب k العناقيد الجديدة. تكرر هذه العملية حتى يحدث التقارب ، أي أن النقاط الوسطى لا تتغير.
كيفية تحديد قيمة K:
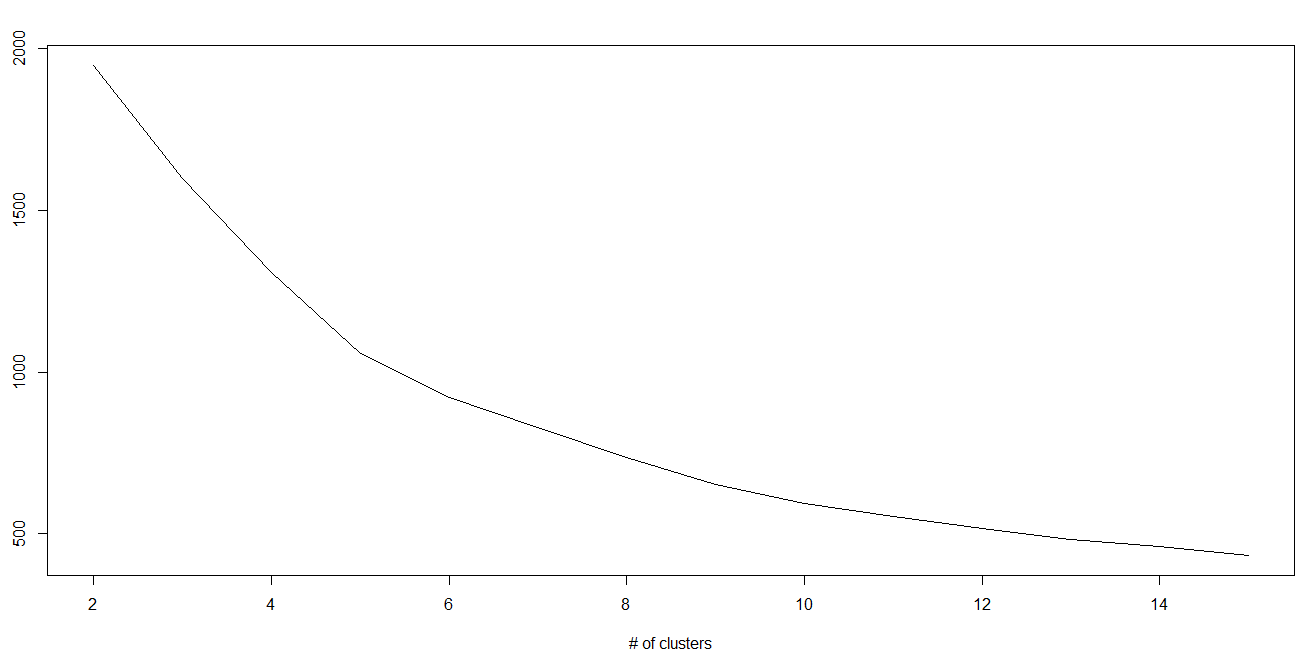
في خوارزمية K-mean ، هناك عناقيد وكل عنقود لها نقطه وسطى centroid خاصة به. مجموع تربيع الفرق بين النقطه الوسطى ونقاط البيانات داخل العنقود يشكل مجموع قيمه مربعه لذلك العنقود. أيضًا ، عند إضافة مجموع القيم المربعة لجميع العناقيد ، يصبح الاجمالي ضمن مجموع القيمة المربعة لحل العنقود.
نعلم أنه مع زيادة عدد العناقيد ، تستمر هذه القيمة في التناقص ولكن إذا قمت برسم النتيجة ، فقد ترى أن مجموع المسافة المربعة يتناقص بشكل حاد إلى قيمة معينة من k ، ثم ببطء بعد ذلك. هنا ، يمكننا إيجاد العدد الأمثل لعدد العناقيد.
مزايا و عيوب خوارزمية K-Means
مزايا خوارزمية K-Means
- سهلة التنفيذ نسبيًا.
- يمكن إستخدامها مع مجموعات بيانات كبيرة.
- تعطي نتائج مرضية
- يمكن تهيئة أماكن النقاط الوسطى مسبقا.
- تتكيف بسهولة مع البيانات الجديدة.
عيوب خوارزمية K-Means
- الاختيار يتم بشكل يدوي باستخدام مخطط “دالة الفقد مقابل عدد العناقيد” للعثور على عدد k الأمثل.
- هذه الخوارزمية تكون معتمدة على القيم الأولية. و من أجل الحصول على قيمة صغيرة ل k ، يمكنك التخفيف من هذا الاعتماد عن طريق تشغيل k-mean عدة مرات بقيم أولية مختلفة واختيار أفضل نتيجة. و مع الزيادة ، تحتاج إلى إصدارات متقدمة من k-mean لاختيار أفضل قيم للنقاط الوسطى الأولية (تسمى k-means seeding).
- تعمل على عنقدة البيانات بأحجام وكثافة متفاوتة. تواجه k-mean مشكلة في تجميع البيانات حيث تكون المجموعات ذات أحجام وكثافة متفاوتة. لتجميع هذه البيانات ، تحتاج إلى تعميم k-mean.
- عنقدة القيم المتطرفة. جيث يمكن سحب و إبعاد القيم الوسطى Centroids بواسطة القيم المتطرفة ، أو قد تحصل القيم المتطرفة على مجموعة خاصة بها بدلاً من تجاهلها. لذلك يجب وضع إزالة القيم المتطرفة أو قصها قبل العنقدة في الاعتبار.
مثال عملي على بايثون
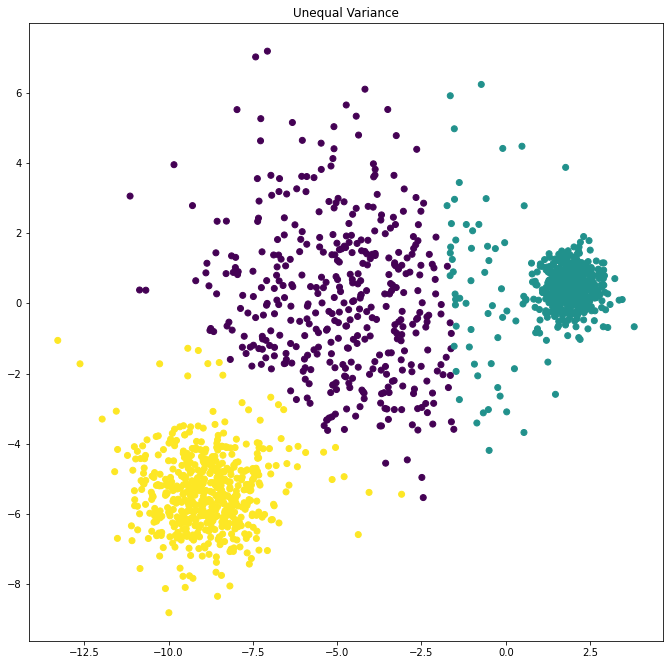
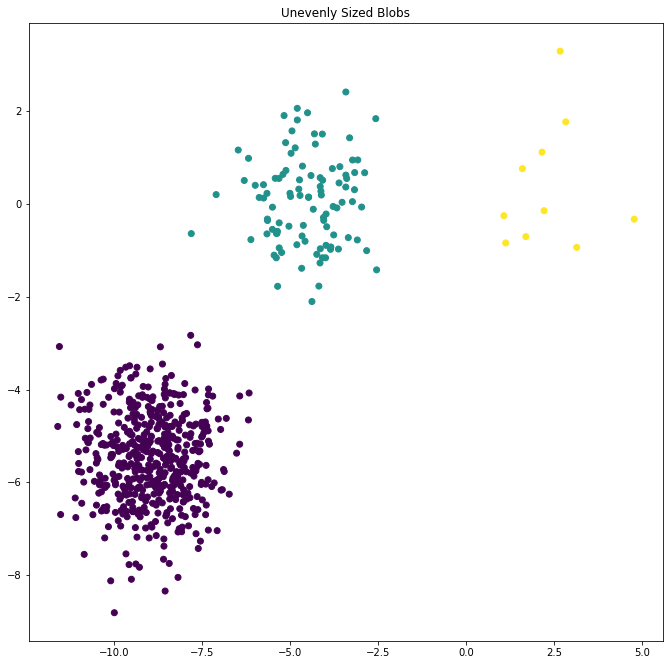
يهدف هذا المثال إلى توضيح الظروف التي ستنتج فيها k-means عناقيد غير بديهية وربما غير متوقعة. في المخططات الثلاثة الأولى ، لا تتوافق بيانات الإدخال مع بعض الافتراضات الضمنية بأن k-means تنتج عناقيد -مجموعات- غير مرغوب كنتيجة . في المخطط الأخير ، تُعيد k-mean عناقيد -مجموعات- بديهية على الرغم من وجود نقاط غير المتساوية الحجم.
أولا: سنعمل على إستيراد المكتبات و البيانات -مكتبات بايثون- الضرورية
import numpy as np مكتبة نامباي للمصفوفات import matplotlib.pyplot as plt مكتبة مات بلوت لب للرسومات البيانية from sklearn.cluster import KMeans إستيراد الخوارزمية from sklearn.datasets import make_blobs إستيراد دالة لإنشاءالبيانات plt.figure(figsize=(12, 12)) ضبط مقاسات الرسم البياني n_samples = 1500 عدد العيانات random_state = 170 اعداد اختيار العينات عشوائيا X, y = make_blobs(n_samples=n_samples, random_state=random_state) انشاء قاعدة بيانات عشوائية
ثانيا: نختير النموذج
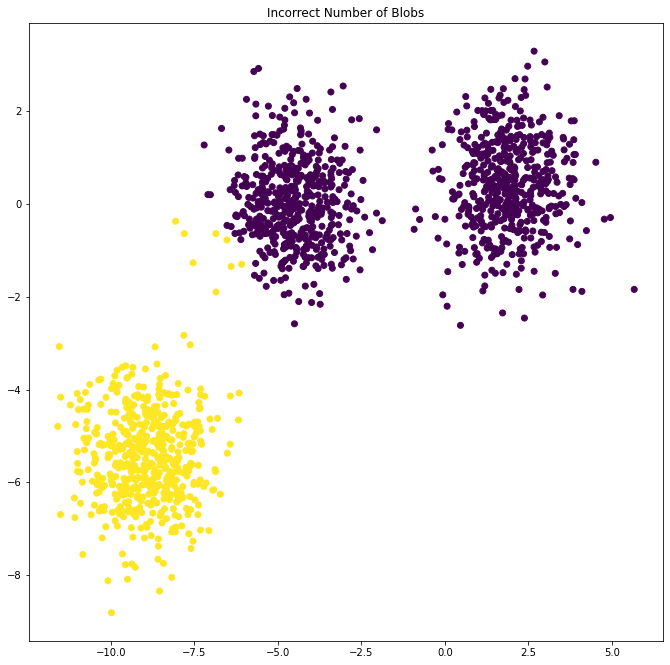
1- في حالة إدخال عدد عناقيد k غير صحيحة
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.title("Incorrect Number of Blobs")
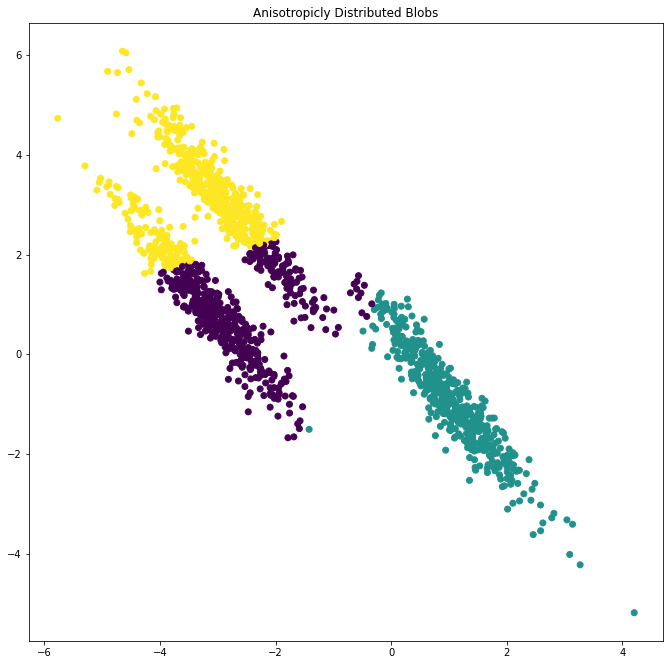
2- في حالة إختبار بيانات موزعة متباينة الخواص
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation) بيانات موزعة متباينة الخواص
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)
plt.subplot(222)
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("Anisotropicly Distributed Blobs")
X_varied, y_varied = make_blobs(n_samples=n_samples,
cluster_std=[1.0, 2.5, 0.5],
random_state=random_state)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)
plt.subplot(223)
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")
4- في حالة النقاط غير المتساوية في الحجم
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10]))
y_pred = KMeans(n_clusters=3,
random_state=random_state).fit_predict(X_filtered)
plt.figure(figsize=(25, 25))
plt.subplot(224)
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs")
plt.show()
المراجع
1- المرجع