شرح مبسط لخوارزمية الغابة العشوائية Random forest و مثال عملي على Python

التصنيف: الذكاء الاصطناعي, تعلم الآلة Machine Learning

تتكون خوارزمية الغابة العشوائية ، كما يوحي إسمها ، من عدد كبير من أشجار القرار Decision Trees الفردية التي تعمل كمجموعة. حيث تنبثق كل شجرة فردية في الغابة العشوائية من توقع الصنف ويصبح الصنف الذي يحصل على أكبر عدد من الأصوات هو توقع النموذج (انظر الشكل أدناه).

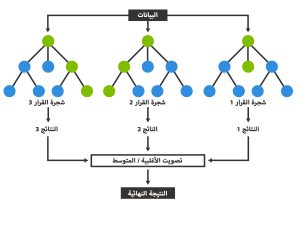
المبدأ الأساسي وراء خوارزمية Random Forest هو مفهوم بسيط الا و هو رأي الأغلبية. السبب وراء نجاح خوارزمية الغابة العشوائية في علم البيانات يرجع الى سبب أن العدد الكبير من النماذج (الأشجار) غير المترابطة نسبيًا التي تعمل كلجنة سيتتفوق على أي نموذج مكون من شجرة قرار واحدة.

إضافة إلى ذلك ، معامل الارتباط المنخفض بين نماذج أشجار القرار هو المفتاح. تمامًا مثل الاستثمارات ذات معامل الارتباط المنخفض (مثل الأسهم والسندات من شركات مختلفة المجالات) التي تشكل المحفظة الإستثمارية. يمكن للنماذج غير المترابطة أن تنتج تنبؤات مجمعة أكثر دقة من أي تنبؤات فردية. سبب هذا التأثير الرائع هو أن الأشجار تحمي بعضها البعض من أخطائها الفردية (طالما أنها لا تخطئ جميعًا في نفس الاتجاه باستمرار). في حين أن بعض الأشجار قد تكون خاطئة ، إلا أن العديد من الأشجار الأخرى ستكون صحيحة ، بحيث يمكن للأشجار كمجموعة أن تتحرك في الاتجاه الصحيح. لذا فإن المتطلبات الأساسية لأداء الغابة العشوائية بشكل جيد هي أنه:

يجب أن تكون هناك بعض الإشارات الفعلية في الميزات بحيث تعمل النماذج المبنية باستخدام هذه الميزات بشكل أفضل من التخمين العشوائي.
يجب أن يكون للتنبؤات التي تقوم بها الأشجار الفردية معامل ارتباط منخفض مع بعضها البعض.

مثال على سبب أفضلية النتائج غير المترابطة

تعتبر التأثيرات الرائعة لامتلاك العديد من النماذج غير المترابطة مفهومًا بالغ الأهمية. تخيل أننا نلعب اللعبة التالية: ستخدم مولد أرقام عشوائي موزع بشكل موحد لإنتاج رقم ما. إذا كان الرقم الذي أنشأته أكبر من أو يساوي 40 ، فأنت تفوز (لذلك لديك فرصة 60٪ للفوز). إذا كان أقل من 40 ، أفوز أنا.

الآن أقدم لك الخيارات التالية. يمكننا إما:

اللعبة 1 – العب 100 مرة ،و المراهنة بدولار واحد في كل مرة.
اللعبة 2 – العب 10 مرات ، و المراهنة على 10 دولارات في كل مرة.
اللعبة 3 – العب مرة واحدة ، و المراهنة على 100 دولار.

أيهما ستختار؟

القيمة المتوقعة لكل لعبة هي نفسها:

القيمة المتوقعة للعبة رقم 1 = (0.60 * 1 + 0.40 * -1) * 100 = 20.
القيمة المتوقعة للعبة رقم 2 = (0.60 * 10 + 0.40 * -10) * 10 = 20.
القيمة المتوقعة للعبة رقم 3 = 0.60 * 100 + 0.40 * -100 = 20.

ماذا عن التوزيعات؟

دعونا نتخيل النتائج من خلال محاكاة خوارزمية مونت كارلو (سنقوم بتشغيل 10000 محاكاة لكل نوع لعبة ؛ على سبيل المثال ، سنقوم بمحاكاة ال 100 لعبة المجودة في اللعبة رقم 1 ، 10000 مرة ). بعد النظر الى الرسم البياني ادناه لتوزيع النتائج ما اللعبة التي ستختارها؟ على الرغم من أن القيم المتوقعة هي نفسها ، إلا أن التوزيعات المرتبطة بالنتائج تختلف اختلافًا كبيرًا من الموجب والضيق (الأزرق) إلى الثنائي (الوردي).

تقدم اللعبة رقم 1 (حيث نلعب 100 مرة) أفضل فرصة لكسب بعض المال. حيث من بين ال 10000 محاكاة التي قمنا بتشغيلها ، يمكنك كسب المال في 97٪ منها! بالنسبة للعبة رقم 2 (حيث نلعب 10 مرات) ، فإنك تكسب المال في 63٪ من المحاكاة ، وهو ما يمثل انخفاضًا حادًا (وزيادة كبيرة في احتمالية خسارة المال). أما بالنسبة لمحاكاة اللعبة رقم 3 ، يمكنك كسب المال في 60٪ من المحاكاة ، كما هو متوقع.

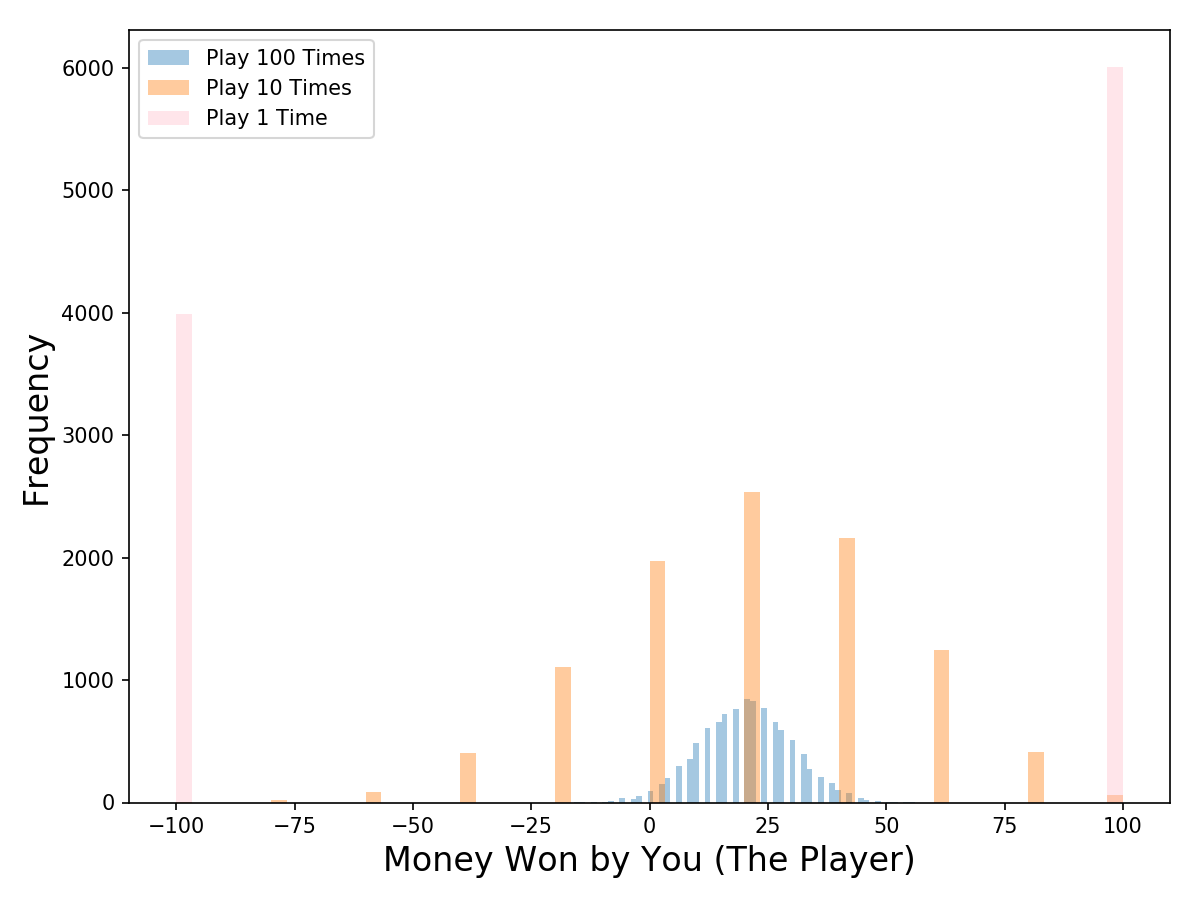
توزيع نتيجة ال 10،000 محاكاة لكل لعبة

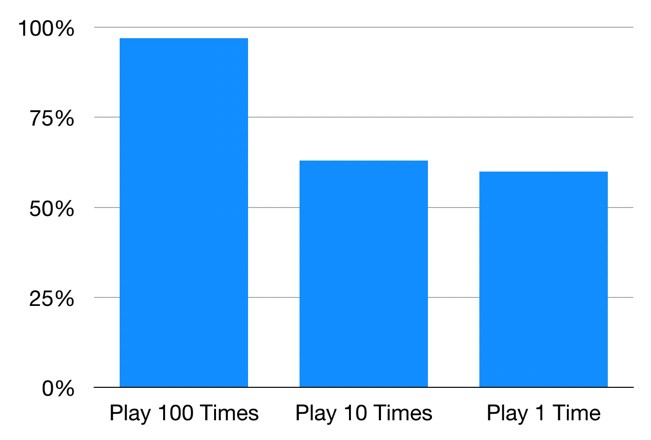احتمالية كسب المال لكل لعبة

لذلك على الرغم من أن الثلاث التجارب تشترك في نفس القيمة المتوقعة ، إلا أن توزيعات نتائجها مختلفة تمامًا. كلما قسمنا رهان ال 100 دولار إلى عدة عمليات مختلفة ، زادت امكانية أننا نكسب المال. كما ذكرنا سابقًا ، هذا يرجع الى استقلالية كل لعبة عن الأخرى.
الغابة العشوائية هي نفسها كل شجرة تشبه لعبة واحدة في لعبتنا هذه . لقد رأينا للتو كيف زادت فرصتنا في كسب المال كلما لعبنا اكثر. و بالمثل ، مع خوارزمية الغابة العشوائية ، تزداد فرصنا في عمل تنبؤات صحيحة مع عدد الأشجار غير المترابطة في الخوارزمية.

مميزات و عيواب خوارزمية الغابة العشوائية

تقلل من فرط التخصيص في أشجار القرار و تساعد على تحسين الدقة و الكفاءة
الخوارزمية تعتبر مرنة لكل من مسائل التصنيف و التنبؤ
تعمل بشكل جيد مع كل من القيم الفئوية و القيم المستمرة
تقوم بأتمتة القيم المفقودة الموجودة في البيانات
ضبط البيانات غير مطلوب في هذه الخوارزمية لأنها تستخدم نهجًا قائمًا على القواعد.

مع ذلك ، على الرغم من هذه المزايا ، فإن خوارزمية الغابة العشوائية لها أيضًا بعض العيوب.

الافتقار إلى القابلية للتفسير: تعتبر الغابات العشوائية بشكل عام نماذج الصندوق الأسود ، مما يعني أنه قد يكون من الصعب فهم كيفية قيام هذه الخوارزومية بتنبؤاتها. قد يكون هذا عيبًا إذا كنت بحاجة إلى شرح الأسباب الكامنة وراء توقع معين لأصحاب المصلحة.
التعقيد الحسابي: يمكن أن تكون الغابات العشوائية مكثفة من الناحية الحسابية ، خاصة إذا كان لديك عدد كبير من الميزات أو الأشجار في الغابة الخاصة بك. هذا يمكن أن يجعلهم أبطأ في التدريب ويصعب توسيع نطاقهم لمجموعات البيانات الكبيرة جدًا.
الافراط في التخصيص: كان من ضمن الايجابيات هو تقليل فرط التخصيص لاشجار القرار لكن يمكن أن تكون الغابات العشوائية عرضة للإفراط في التخصيص ، خاصة إذا كنت تستخدم عددًا كبيرًا من الأشجار أو إذا كان لديها ميزات عالية الأبعاد. يمكن أن يؤدي هذا إلى نماذج تعمل بشكل جيد على بيانات التدريب ولكن بشكل سيئ على بيانات الاختبار.
التحيز تجاه الميزات ذات المستويات المتعددة: تميل الغابات العشوائية إلى تفضيل الميزات ذات المستويات أو الفئات المتعددة ، مما قد يؤدي إلى زيادة التخصيص على هذه الميزات وعدم ملاءمة الآخرين.
صعوبة التعامل مع البيانات غير المتوازنة: يمكن أن تعاني الغابات العشوائية مع مجموعات البيانات غير المتوازنة ، حيث تكون إحدى الفئات أكثر شيوعًا من الفئات الأخرى. يمكن أن يؤدي هذا إلى نماذج ذات دقة عالية في فئة الأغلبية ولكن دقة ضعيفة في فئات الأقليات.

تطبيق خوارزمية الغابات العشوائية على مسائل التنبؤ

من أجل التنبؤ، سنتعامل مع البيانات التي تحتوي على رواتب الموظفين بناءً على مناصبهم. سنستخدم هذا للتنبؤ براتب الموظف بناءً على منصبه.

أولا لنستورد المكتبات و البيانات

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv(‘Salaries.csv')
df.head()
X =df.iloc[:, 1:2].values
y =df.iloc[:, 2].values

ثانيا نظرا لصغر حجم قاعدة البيانات فلن نقسمهما الى مجموعة تدريب و مجموعة إختبار و نستورد خوارزمية الغابة العشوائية و نعمل على ملائمة النموذج على البيانات

from sklearn.ensemble 
import RandomForestRegressor
model = RandomForestRegressor(n_estimators = 10, random_state = 0)
model.fit(X, y)

هل لاحظت أننا وضعنا 10 أشجار فقط بكتابة n_estimators = 10 على الكود؟ الأمر متروك لك لإختيار عدد الأشجار المناسب. لكن نظرًا لأنها مجموعة البيانات صغيرة ، فإن 10 أشجار كافية.

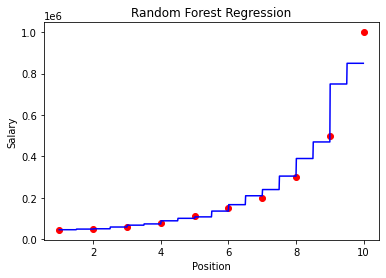
ثالثا سنتنبأ براتب شخص لديه المستوى 6.5 , فنلاحظ بعد رسم الرسم البياني أن الموظف يجب أن يحصل على راتب قدره 167000 بعد وصوله إلى مستوى 6.5.

y_pred =model.predict([[6.5]]) X_grid_data = np.arange(min(X), max(X), 0.01)
X_grid_data = X_grid.reshape((len(X_grid_data), 1))
plt.scatter(X, y, color = 'red')
plt.plot(X_grid_data,model.predict(X_grid_data), color = 'blue')
plt.title('Random Forest Regression’)
plt.xlabel('Position')
plt.ylabel('Salary')
plt.show()