في هذا المقال سنتعرف على طريقة المربعات الصغرى الخطية Ordinary Least Squares المستخدمة في تقدير معاملات دالة الإنحدار الخطي Linear Regression. سنتعرف على تعريف هذه الطريقة. ثم سنتعرف على المعادلات المستخدمة في هذه الطريقة. و أخيرا سنتعرف على ميزات و عيوب هذه الطريقة.
المربعات الصغرى الخطية Ordinary least squares او OLS هي طريقة تستخدم لتقدير معلمات نموذج الانحدار الخطي Linear Regression الذي يقلل من مجموع القيم المربعة بين القيم المتوقعة والقيم الفعلية. بمعنى آخر ، تجد طريقة OLS الخط الأفضل ملاءمة من خلال مجموعة من نقاط البيانات عن طريق تقليل مجموع تربيع الفروق بين القيم المتوقعة و القيم الفعلية.
المعادلة العامة لنموذج الانحدار الخطي بمتغير مستقل واحد (x) ومتغير تابع واحد (y) هي:
y = β0 + β1x + ε
حيث β0 هو التقاطع بين خط الإنحدار و المحور الرأسي ، و β1 هو الميل ، و هو مصطلح الخطأ كما هو موضح أدناه. الهدف من طريقة OLS هو تقدير قيم β0 و β1 التي تقلل من مجموع الأخطاء التربيعية. حيث يتم حساب قيم β0 و β1 بإستخدام المعادلتين التاليتين:
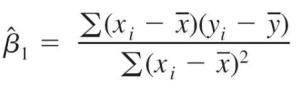
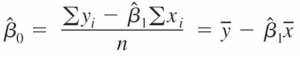
حيث n: عدد العينات ، x_i و y_i: قيم المتغيرات المستقلة والمتغيرات التابعة للعينة ، x̄: متوسط قيم المتغيرات المستقلة.
طريقة OLS هي طريقة مستخدمة على نطاق واسع لتقدير معلمات نماذج الانحدار الخطي لأنها سهلة الفهم والتنفيذ. أيضا توفر تقديرات غير متحيزة وفعالة لمعاملات الانحدار في ظل افتراضات معينة. ومع ذلك ، تفترض طريقة OLS أن الأخطاء يتم توزيعها بشكل طبيعي ولها تباين ثابت. وهذا يتعارض لما هو الحال في الواقع. في مثل هذه الحالات ، قد تكون الطرق الأخرى أكثر ملاءمة. مثال على ذلك طريقتي المربعات الصغرى الموزونة weighted least squares أو الانحدار القوي robust regression.