خوارزمية النزول الإشتقاقي Gradient Descent تعتبر من أهم خوارزميات التحسين. حيث أنها تُستخدم بشكل شائع لتدريب نماذج التعلم الآلي والشبكات العصبية. بالاضافة إلى أنها تساعد بيانات تدريب هذه النماذج على التعلم بمرور الوقت. و تعمل دالة الفقد ضمن نزول إشتقاقي على وجه التحديد كمقياس ، وتقيس دقتها مع كل تكرار لتحديثات المعلمات. حتى تقترب الدالة من الصفر أو تساويها ،حيث يستمر النموذج في ضبط معلماته للحصول على أصغر خطأ ممكن.
كيف تعمل خوارزمية النزول الاشتقاقي
قبل الغوص في خوارزمية النزول الإشتقاقي ، قد يكون من المفيد مراجعة بعض المفاهيم من الانحدار الخطي. قد تتذكر الصيغة التالية لميل الخط ، وهي y=mx+b ، حيث يمثل m الميل ويمثل b نقطة التقاطع على المحور y.
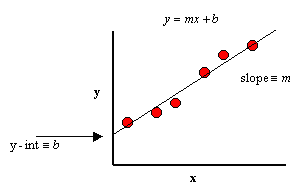
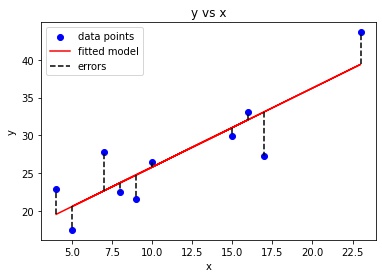
قد تتذكر أيضًا الرسم البياني للنقاط المبعثرة scatter plot في الإحصاء وإيجاد خط أفضل ملاءمة. الأمر الذي يتطلب حساب الخطأ بين القيمة الفعلية (y) والقيمة المتوقعة (y-hat) باستخدام معادلة متوسط الخطأ التربيعي. تعمل خوارزمية النزول الإشتقاقي بشكل مشابه ، لكنها تستند إلى دالة محدبة convex function.
خوارزمية النزول الإشتقاقي تبدأ بنقطة البداية starting point و هي مجرد نقطة اعتباطية لتقييم الأداء. و من نقطة البداية هذه ، سنحسب الإشتاق (أو الميل). ومن هناك ، يمكننا استخدام خط المماس لملاحظة انحدار المنحدر. سيعمل الميل على تحديث قيم المعلمات أي الأوزان و التحيزات. سيكون الميل عند نقطة البداية أكثر حدة. و لكن مع إنشاء معلمات جديدة ، سينخفض الميل تدريجيًا حتى يصل إلى أدنى نقطة على المنحنى. و هذه النقطة تعرف باسم نقطة التقارب point of convergence.
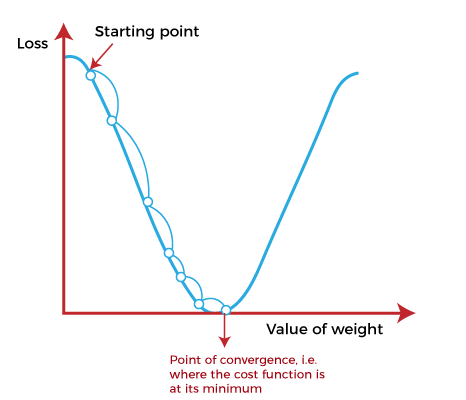
على غرار العثور على الخط الأنسب في الانحدار الخطي ، فإن الهدف من خوارزمية النزول الإشتقاقي هو تقليل قيمة دالة الفقد. و من أجل القيام بذلك ، فإننا نحتاج إلى عاملين مهمين هما الاتجاه و معدل التعلم. تحدد هذه العوامل الحسابات المشتقة الجزئية للتكرارات المستقبلية. و هذا يسمح لها بالوصول تدريجيًا إلى الحد الأدنى الموضعي أو العام.
معدل التعلم
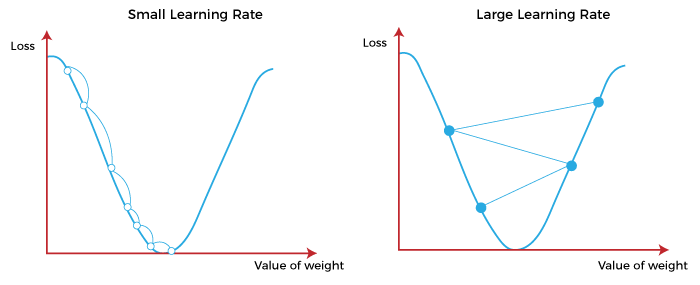
(يشار إليه أيضًا باسم حجم الخطوة أو ألفا) هو حجم الخطوات التي يتم اتخاذها للوصول إلى الحد الأدنى. عادةً ما تكون هذه القيمة صغيرة ، ويتم تقييمها وتحديثها بناءً على سلوك دالة الفقد. تؤدي معدلات التعلم المرتفعة إلى خطوات أكبر ولكنها تخاطر بتجاوز الحد الأدنى. على العكس من ذلك ، فإن معدل التعلم المنخفض له أحجام خطوات صغيرة. و على الرغم من أنها تتميز بمزيد من الدقة ، إلا أن عدد التكرارات يضر بالكفاءة الكلية. و ذلك لأن عدد التكرارات الكبير يستغرق المزيد من الوقت والحسابات للوصول إلى الحد الأدنى. الشكل أدناه يوضح تأثير معدلات التعلم العالية و معدلات المنخفضة على دالة الفقد.
دالة الفقد أو دالة التكلفة
تقيس الفرق ، أو الخطأ ، بين قيم y الفعلية و قيم y المتوقعة. تعمل هذه الدالة على تحسين فعالية نموذج التعلم الآلي. و ذلك من خلال تقديم ملاحظات للنموذج حتى يتمكن من ضبط المعلمات لتقليل الخطأ وإيجاد الحد الأدنى الموضعي أو العام. إنها عملية متكررة باستمرار ، وتتحرك على طول اتجاه أقصى نزول (أو التدرج الإشتقاقي السالب) حتى تقترب دالة التكلفة من الصفر أو عنده. في هذه المرحلة ، سيتوقف النموذج عن التعلم. بالإضافة إلى ذلك ، في حين ان البعض يعتبر المصطلحين دالة التكلفة و دالة الفقد مترادفين ، إلا أن هناك اختلافًا طفيفًا بينهما. و هذا الاختلاف هو أن دالة الفقد تشير إلى خطأ في مثال تدريب واحد ، بينما تحسب دالة التكلفة متوسط الخطأ عبر مجموعة تدريب كاملة.
انواع خوارزمية النزول الاشتقاقي
-
خوارزمية النزول الإشتقاقي العشوائي Stochastic Gradient Descent
عبارة عن خوارزمية تحسين بسيطة تقوم بتحديث أوزان الشبكة باستخدام التدرج الإشتقاقي لدالة الفقد مع الأخذ بعين الإعتبار قيمة الأوزان. هذه الخوارزمية تعتبر أيضا خوارزمية عشوائية. مما يعني أنها تقوم بتحديث الأوزان باستخدام عينة عشوائية من البيانات بدلاً من مجموعة البيانات بأكملها. حيث تدير هذه الخوارزمية دورة epoch تدريب لكل مثال ضمن مجموعة البيانات. ثم تقوم بتحديث معلمات كل مثال تدريبي واحدًا تلو الآخر. نظرًا لأنننا تحتاج فقط إلى الاحتفاظ بمثال تدريبي واحد ، فمن السهل تخزينها في الذاكرة. في حين أن هذه التحديثات المتكررة يمكن أن توفر مزيدًا من التفاصيل و تزيد من سرعة التدريب إلا أنها قد تؤدي إلى فقد في الكفاءة الحسابية عند مقارنتها بخوارزمية النزول الإشتقاقي الحزمي. يمكن أن تؤدي تحديثاتها المتكررة إلى تدرجات متطرفة. ولكن هذا يمكن أن يكون مفيدًا في ايجاد الحد الأدنى العام على حساب الحد الادنى الموضعي. قاعدة التحديث للأوزان لخوارزمية النزول الإشتقاقي العشوائي Stochastic Gradient Descent تعطى بالمعادلة التالية:
w = w – η ∇J(w)
حيث w هو الوزن ، η هو معدل التعلم ، و J(w)∇ هو التدرج الإشتقاقي لدالة الفقد مع الأخذ بعين الإعتبار الوزن w.

-
خوارزمية النزول الإشتقاقي الحزمي Batch Gradient Descent
هي خوارزمية تحسين تُستخدم لتحديث معلمات نموذج التعلم الآلي. يطلق عليها نزول إشتقاقي “حزمي” لأنها تستخدم مجموعة بيانات التدريب بالكامل لحساب التدرج الإشتقاقي gradient لدالة الفقد في كل تكرار. الفكرة الأساسية وراء هذه الخوارزمية هي حساب التدرج الإشتقاقي gradient لدالة الفقد فيما يتعلق بمعلمات النموذج واستخدام بيانات التدرج الإشتقاقي هذه لتحديث المعلمات في اتجاه التدرج الإشتقاقي السالب ، من أجل تقليل قيمة دالة الفقد. تجمع الخوارزمية نسب الخطأ لكل نقطة في مجموعة بيانات التدريب ، مع تحديث النموذج فقط بعد تقييم جميع أمثلة التدريب. على الرغم من أن هذا التجميع يوفر كفاءة حسابية ، إلا أنه لا يزال من الممكن أن يستغرق وقتًا طويلاً في المعالجة لمجموعات بيانات التدريب الكبيرة حيث لا يزال يحتاج إلى تخزين جميع البيانات في الذاكرة. عادةً ما ينتج عن خوارزمية النزول الإشتقاقي الحزمي أيضًا تدرجًا ثابتًا للخطأ وتقاربًا. ولكن في بعض الأحيان لا تكون نقطة التقارب هذه هي الأكثر مثالية. و ذلك حيث يتم إيجاد الحد الأدنى الموضعي على حساب الحد الأدنى العام. يتم حساب التدرج الإشتقاقي gradient باستخدام بيانات التدريب بأكملها. يمكن كتابة قاعدة التحديث للمعلمات في هذه الخوارزمية على النحو التالي:
w_t = w_t-1 – η ∇L(w_t-1)
حيث w_t هو الوزن المحدث ، w_t-1 هو الوزن السابق ، η هو معدل التعلم ، و L(w_t-1)∇ هو التدرج الإشتقاقي لدالة الفقد مع الأخذ بعين الإعتبار الوزن w.
من المعروف أن خوارزمية النزول الإشتقاقي الحزمي Batch Gradient Descent تعمل بشكل بطيئ عندما تكون مجموعة البيانات كبيرة. حيث يتطلب ذلك حساب التدرج الإشتقاقي gradient لدالة الفقد باستخدام مجموعة البيانات بأكملها في كل تكرار. يمكن أن يكون هذا مكلفًا من الناحية الحسابية ، ولكن له ميزة ضمان التقارب مع الحد الأدنى لدالة الفقد global minimum، في ظل ظروف معينة ، مثل دالة الفقد المحدبة convex loss function ومعدل التعلم الذي يتناقص بمرور الوقت.
-
خوارزمية النزول الإشتقاقي الحزمي المصغر Mini-Batch Gradient Descent
عبارة عن خوارزمية تحسين تندرج تحت خوارزمية النزول الإشتقاقي العشوائي Stochastic Gradient Descent. هذه الخوارزمية تقوم بتحديث معلمات النموذج باستخدام مجموعة فرعية عشوائية صغيرة من بيانات التدريب (حزمة صغيرة mini-batch) بدلاً من استخدام جميع بيانات التدريب في كل تكرار. الفكرة وراء ذلك هي أن تقريب الحزمة المصغرة للتدرج الإشتقاقي تكون أكثر كفاءة من الناحية الحسابية ويمكن أن تؤدي إلى تحسين النموذج جيدا. قاعدة التحديث في خوارزمية النزول الإشتقاقي الحزمي المصغر Mini-Batch Gradient Descent مماثلة لتلك الخاصة بـخوارزمية النزول الإشتقاقي العشوائي Stochastic Gradient Descent:
w_t = w_t-1 – η ∇L(w_t-1)
حيث w_t هو الوزن المحدث ، w_t-1 هو الوزن السابق ، η هو معدل التعلم ، و L(w_t-1)∇ هو التدرج الإشتقاقي لدالة الفقد مع الأخذ بعين الإعتبار الوزن w.
يمكن أن تؤدي هذه الخوارزمية إلى تقارب أسرع مقارنةً بخوارزمية النزول الإشتقاقي الحزمي Batch Gradient Descent كما أنه أكثر قوة للبيانات المليئة بالبيانات المتطرفة مقارنةً بخوارزمية النزول الإشتقاقي العشوائي Stochastic Gradient Descent. حجم الحزمة المصغرة عبارة عن معلمة تشعبية يمكن ضبطها للعثور على أفضل مفاضلة بين وقت الحساب ودقة التحسين.
الاختلاف الرئيسي بين خوارزميتي النزول الإشتقاقي الحزمي و النزول الإشتقاقي الحزمي المصغر
يكمن الاختلاف الرئيسي بين خوارزميتي النزول الإشتقاقي الحزمي و النزول الإشتقاقي الحزمي المصغر في عدد أمثلة التدريب المستخدمة لتحديث معلمات النموذج في كل تكرار.
في خوارزمية النزول الإشتقاقي الحزمي ، يتم تحديث معلمات النموذج باستخدام التدرج الإشتقاقي لدالة الفقد المحسوبة على مجموعة بيانات التدريب بأكملها. هذا يعني أن كل تكرار يستغرق وقتًا أطول لإكماله. و لكن بيانات التدرج المستخدمة لتحديث المعلمات أكثر دقة. ومع ذلك ، يمكن أن تكون خوارزمية النزول الإشتقاقي الحزمي مكلفة حسابيًا وبطيئة في التقارب عندما تكون مجموعة بيانات التدريب كبيرة جدًا.
في خوارزمية النزول الإشتقاقي الحزمي المصغر ، يتم تحديث معلمات النموذج باستخدام التدرج الإشتقاقي لدالة الفقد المحسوبة على مجموعة فرعية عشوائية صغيرة من بيانات التدريب ، تسمى الحزمة المصغرة. حجم الحزمة المصغرة عبارة عن معلمة تشعبية يتم تعيينها عادةً على قيمة تتراوح بين 10 و 1000 ، اعتمادًا على حجم مجموعة بيانات التدريب والموارد الحسابية المتاحة. تعد خوارزمية النزول الإشتقاقي الحزمي المصغر أسرع من خوارزمية النزول الإشتقاقي الحزمي لأنها تتطلب عددًا أقل من العمليات الحسابية في كل تكرار ، ولكن بيانات التدرج الإشتقاقي المستخدمة لتحديث المعلمات تكون أكثر تطرفا فيها من خورازمة النزول الإشتقاقي الحزمي.
لكل من الخوارزميتين مزايا وعيوب. و يعتمد الاختيار بينهما على حجم مجموعة بيانات التدريب و الموارد الحسابية المتاحة والمفاضلة المطلوبة بين سرعة التحسين ودقة التحسين. من الناحية العملية ، غالبًا ما تستخدم خوارزمية النزول الإشتقاقي الحزمي المصغر في تطبيقات التعلم الآلي واسعة النطاق ، حيث توفر توازنًا جيدًا بين الكفاءة الحسابية ودقة التحسين.