تعد الشبكة العصبية الاصطناعية ANN ، نوع من نماذج التعلم الآلي المستوحاة من بنية و وظيفة الدماغ البشري. يتكون من طبقات من العقد المترابطة أو الخلايا العصبية الاصطناعية ، والتي تتلقى المدخلات ، تجري حسابات رياضية ، وتنتج المخرجات. تتكون الشبكات العصبية من ثلاث طبقات رئيسية طبقتي المدخلات input layer و المخرجات output layer، بالإضافة إلى طبقة أو طبقات مخفية hidden layer/s. و تقوم هذه الشبكات بأداءً جيدًا في المهام التي تتطلب إيجاد أنماط. تُستخدم شبكات ANN في مجموعة متنوعة من التطبيقات ، مثل التعرف على الصور و الكلام و معالجة اللغة الطبيعية و السيارات ذاتية القيادة و غير ذلك.
يتم تدريب الشبكات العصبية الاصطناعية ANN باستخدام مجموعات بيانات كبيرة و خوارزميات تضبط نقاط قوة الاتصالات بين الخلايا العصبية لتقليل الفقد بين المخرجات المتوقعة و الفعلية. بمجرد التدريب ، يمكن لشبكات ANN إجراء تنبؤات أو تصنيفات على بيانات جديدة غير مرئية.
في حين أن هناك الكثير من خوارزميات الذكاء الاصطناعي هذه الأيام ، فإن الشبكات العصبية قادرة على أداء ما يسمى التعلم العميق. في حين أن الوحدة الأساسية للدماغ هي الخلايا العصبية ، فإن اللبنة الأساسية للشبكة العصبية الاصطناعية هي المستشعر الذي ينجز معالجة بسيطة للإشارات ، ثم يتم توصيلها بشبكة خلايا كبيرة.
يتم تعليم الكمبيوتر المزود بالشبكة العصبية القيام بمهمة من خلال جعله يحلل أمثلة التدريب ، والتي يتم تصنيفها مسبقًا. من الأمثلة الشائعة على أستخدامات الشبكات العصبية باستخدام التعلم العميق مثال التعرف على صور الكائنات، حيث يتم تقديم الشبكة العصبية بعدد كبير من الكائنات من نوع معين ، مثل قطة ، أو لافتة شارع ، والكمبيوتر ، من خلال تحليل الأنماط المتكررة في الصور المعروضة ، يتعلم تصنيف الصور الجديدة.
مقدمة
الشبكات العصبية عبارة عن شبكات متعددة الطبقات من الخلايا العصبية التي تستخدم لتصنيف الأشياء وعمل التنبؤات وما إلى ذلك. يوجد أدناه مخطط لشبكة عصبية بسيطة تحتوي على خمسة مدخلات و خمسة مخرجات بالإضافة إلى طبقتين مخفيتين من الخلايا العصبية.
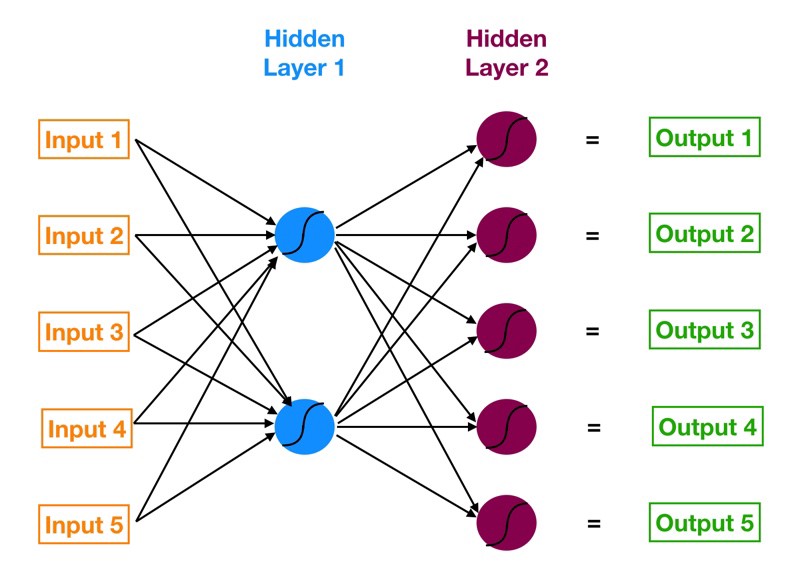
بدءًا من اليسار ، لدينا:
طبقة المدخلات باللون البرتقالي.
أول طبقة مخفية من الخلايا العصبية باللون الأزرق.
ثاني طبقة مخفية من الخلايا العصبية باللون الأرجواني.
طبقة المخراجات باللون الأخضر.
توضح الأسهم التي تربط النقاط كيف أن جميع الخلايا العصبية مترابطة وكيف تنتقل البيانات من طبقة الإدخال على طول الطريق إلى طبقة الإخراج.
طريقة عمل الشبكات العصبية
لفهم طريقة عمل الشبكات العصبية ، دعونا أولا نسأل ما الذي تحاول الشبكة العصبية فعله بالضبط؟ الإجابة بالطبع مثل أي نموذج آخر، الشبكات العصبية تحاول العمل على إنجاز تنبؤ جيد. لدينا مجموعة من المدخلات ومجموعة من القيم المستهدفة – ونحاول الحصول على تنبؤات تتطابق مع تلك القيم المستهدفة بأكبر قدر ممكن.
لتوضيح الصورة أكثر انسَ لثانية الصورة الأكثر تعقيدًا للشبكة العصبية التي رسمناها أعلاه وركز على الصورة المبسطة أدناه.
الإنحدار اللوجستي ذو الميزة الواحدة (المتغير X في الشكل أعلاه) يمكن التعبير عنه من خلال شبكة عصبية ذول مدخل واحد. لمعرفة كيفية إتصال الخلايا يمكننا إعادة كتابة معادلة نموذج الانحدار اللوجستي باستخدام رموز ألوان الشبكة العصبية الخاصة بنا.
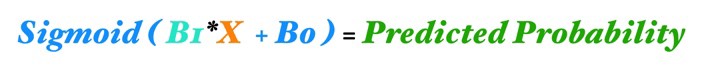
دعونا نفك رموز كل عنصر:
- X (باللون البرتقالي) يرمز إلى طبقة المدخلات ، وهي الميزة الوحيدة التي نقدمها لنموذجنا من أجل حساب التنبؤ.
- B1 (باللون الفيروزي) يرمز إلى معلمة الإنحدار المقدرة للإنحدار اللوجستي لهذا المثال – تخبرنا B1 بمدى تغير Log_Odds مع تغير X. لاحظ أن B1 توجد على الاتصال – الخط الفيروزي – الذي يربط خلية X في طبقة المدخلات بالخلية العصبية الزرقاء في الطبقة المخفية Hidden Layer 1.
- B0 (باللون الأزرق) يرمز إلى معلمة التحيز – مشابه جدًا لمصطلح التقاطع في الانحدار الخطي. الفرق الرئيسي هو أنه في الشبكات العصبية ، لكل خلية عصبية مصطلح تحيز خاص بها (بينما في الانحدار ، يكون للنموذج مصطلح تقاطع فردي واحد).
- تتضمن الخلايا العصبية المرمزة باللون الأزرق أيضًا دالة تنشيط سينية (يُشار إليها بالخط المنحني داخل الدائرة الزرقاء).
- وأخيرًا نحصل على الاحتمالية المتوقعة من خلال تطبيق الدالة السينية sigmoid function على الكمية (B1 * X + B0).
ليس صعبا للغاية ، أليس كذلك؟ . تتكون الشبكة العصبية المبسطة من المكونات التالية فقط:
- إتصال (على الرغم من أنه من الناحية العملية ، سيكون هناك بشكل عام وصلات متعددة ، لكل منها وزنها الخاص ، وتنتقل إلى خلية عصبية معينة) ، مع وجود أوزان مرتبطة بها ، والذي يحول المدخلات (باستخدام B1) ويوصلها للخلايا العصبية .
- خلية عصبية تتضمن مصطلح التحيز (B0) و دالة التنشيط sigmoid function.
وهذان الجسمان هما اللبنات الأساسية للشبكة العصبية. الشبكات العصبية الأكثر تعقيدًا هي عبارة عن نماذج ذات طبقات مخفية أكثر وهذا يعني المزيد من الخلايا العصبية والمزيد من الروابط بين الخلايا العصبية. وهذه الشبكة الأكثر تعقيدًا من الاتصالات (والأوزان والتحيزات) هي ما يسمح للشبكة العصبية “بتعلم” العلاقات المعقدة المخفية في البيانات الكبيرة.
دعونا نضيف القليل من التعقيد الآن
الآن بعد أن فهمنا الأساسيات في مبدأ و طريقة عمل الشبكات العصبية ، دعونا نعود إلى شبكتنا العصبية الأكثر تعقيدًا بعض الشيء ونرى كيف تنتقل البيانات من المدخلات إلى المخرجات. بالنظر إلى الرسم أعلاه تتكون الطبقة الأولى المخفية من خليتين عصبيتين. لربط جميع المدخلات الخمسة بالخلايا العصبية في الطبقة المخفية Hidden Layer 1 ، نحتاج إلى عشرة اتصالات. تُظهر الصورة التالية (أدناه) الروابط بين طبقة المدخلات 1 والطبقة المخفية 1 فقط.
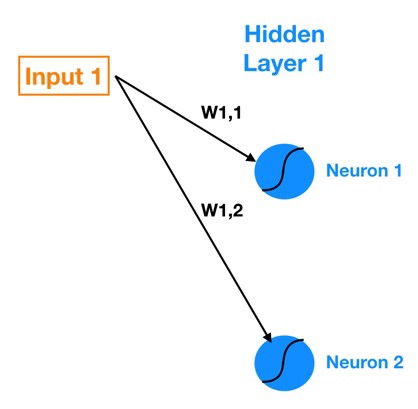
لاحظ تدويننا للأوزان التي توجد في الوصلات – يشير W1،1 إلى وزن الصلة بين input 1 و Neuron 1 و W1،2 يشير إلى الوزن في الصلة بين input 1 و Neuron 2. لذا فإن الترميز العام الذي سأتبعه هو Wa،b يشير إلى الوزن على العلاقة بين input a و Neuron b.
الآن دعونا نحسب مخرجات كل خلية عصبية في Hidden Layer 1 (المعروفة باسم التنشيط Activation). نقوم بذلك باستخدام الصيغ التالية (يشير W إلى الوزن ، ويشير In إلى input).
Z1 = W1*In1 + W2*In2 + W3*In3 + W4*In4 + W5*In5 + Bias_Neuron1
يمكننا استخدام المصفوفة لتلخيص هذا الحساب (تذكر قواعد الترميز الخاصة بنا – على سبيل المثال ، يشير W4،2 إلى الوزن الموجود في الصلة بين (input 4 و Neuron 2):
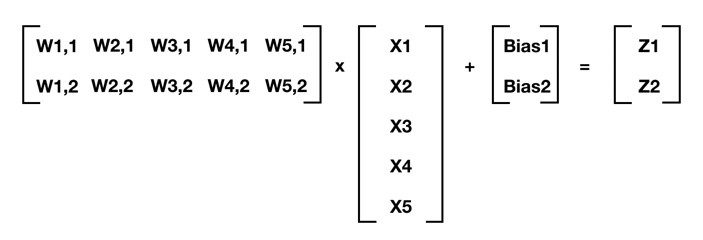
بالنسبة لأي طبقة من الشبكة العصبية تكون فيها الطبقة السابقة ذو أبعاد m من العناصر والطبقة الحالية بأبعاد n من العناصر ، فإن هذا يعمم على:
[W] * [X] + [Bias] = [Z]
حيث أن [W] هي مصفوفة الأوزان الخاصة بالشبكة n × m (الصلات بين الطبقة السابقة والطبقة الحالية) ، [X] هي مصفوفة m في 1 مصفوفة إما لمدخلات البداية أو التنشيط من الطبقة السابقة ، [Bias] هو n في 1 مصفوفة من تحيزات الخلايا العصبية ، و [Z] هي مصفوفة n من 1 من النواتج الوسيطة. في المعادلة السابقة. بمجرد أن نحصل على [Z] ، يمكننا تطبيق دالة التنشيط (السيني في حالتنا) على كل عنصر من [Z] وهذا يعطينا مخرجات الخلايا العصبية (التنشيط) للطبقة الحالية.
أخيرًا قبل أن ننتقل للخطوة التالية ، دعنا نضع كل عنصر من هذه العناصر مرئية مرة أخرى على مخطط الشبكة العصبية لربطها كلها ([التحيز] مضمن في الخلايا العصبية الزرقاء).
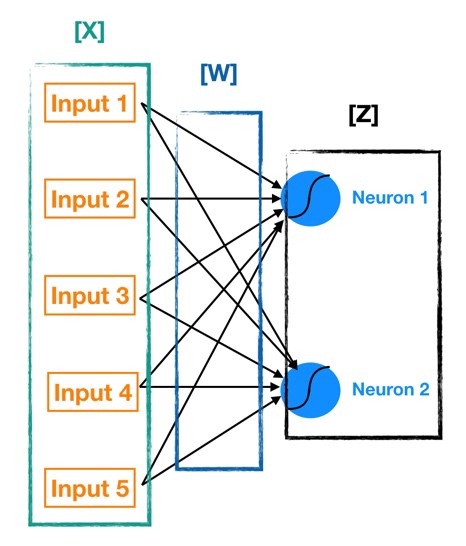
من خلال حساب [Z] بشكل متكرر وتطبيق دالة التنشيط عليها لكل طبقة متتالية ، يمكننا الانتقال من طبقة الإدخال إلى طبقة الإخراج. تُعرف هذه العملية بالانتشار الأمامي Forward propagation. الآن بعد أن عرفنا كيفية حساب المخرجات ، حان الوقت للبدء في تقييم جودة المخرجات وتدريب الشبكة العصبية.
حان الوقت لتعليم الشبكة العصبية
الآن بعد أن عرفنا كيف يتم حساب قيم مخرجات الشبكة العصبية ، حان الوقت لتدريبها. تشبه عملية التدريب للشبكة العصبية ، على مستوى عالٍ ، تلك الخاصة بالعديد من نماذج علوم البيانات الأخرى – حدد دالة التكلفة cost function واستخدم gradient descent optimization لتقليلها.
أولاً ، دعنا نفكر في الرافعات levers التي يمكننا سحبها لتقليل دالة التكلفة. في الانحدار الخطي أو اللوجستي التقليدي ، نبحث عن معاملات بيتا (B0 ، B1 ، B2 ، إلخ) التي تقلل من دالة التكلفة. بالنسبة للشبكة العصبية ، نقوم بنفس الشيء ولكن على نطاق أكبر وأكثر تعقيدًا.
في الانحدار التقليدي ، يمكننا تغيير أي بيتا معين بمعزل دون التأثير على معاملات بيتا الأخرى. لذلك من خلال تطبيق تغييرات صغيرة معزولة على كل معامل بيتا وقياس تأثيره على دالة التكلفة ، فمن السهل نسبيًا تحديد الاتجاه الذي نحتاج إلى التحرك فيه لتقليل دالة التكلفة وتقليلها في النهاية.
في الشبكة العصبية ، يكون لتغيير وزن أي اتصال واحد (أو انحياز خلية عصبية) تأثير صدى عبر جميع الخلايا العصبية الأخرى وتنشيطها في الطبقات اللاحقة.
ذلك لأن كل خلية عصبية في الشبكة العصبية تشبه نموذجها الصغير الخاص. على سبيل المثال ، إذا أردنا انحدارًا لوجستيًا من خمس سمات ، فيمكننا التعبير عنه من خلال شبكة عصبية ، مثل تلك الموجودة على اليسار ، باستخدام خلية عصبية واحدة فقط!
لذا فإن كل طبقة مخفية من الشبكة العصبية هي في الأساس مجموعة من النماذج (كل خلية عصبية فردية في الطبقة تعمل مثل نموذجها الخاص) التي تغذي مخرجاتها المزيد من النماذج اللاحقة (كل طبقة مخفية متتالية من الشبكة العصبية تحمل المزيد من الخلايا العصبية) .
دالة التكلفة Cost Function
دالة التكلفة في الواقع ليست بهذات الصعوبة. لنأخذ الأمر خطوة بخطوة. أولاً بالنظر إلى مجموعة من مدخلات التدريب (الميزات) والنتائج (الهدف الذي نحاول توقعه):
نريد العثور على مجموعة الأوزان (تذكر أن كل خط ربط بين أي عنصرين في الشبكة العصبية يحتوي على وزن) والتحيزات (كل خلية عصبية تحتوي على تحيز) تقلل من دالة التكلفة لدينا – حيث تكون دالة التكلفة تقريبًا لكيفية خاطئة توقعاتنا تتعلق بالنتيجة المستهدفة.
لتدريب شبكتنا العصبية ، سوف نستخدم متوسط الخطأ التربيعي (MSE) كدالة تكلفة:
MSE = مجموع[ (التنبؤ – القيمة_الفعلية)²] * (1/ عدد_الملاحظات)
يخبرنا MSE للنموذج في المتوسط كم نسبة الخطأ في النموذج بحيث نعاقب التنبؤات البعيدة عن القيمة الحقيقية بشدة أكثر من تلك التي تكون بعيدة قليلاً. تعمل دالة التكلفة للانحدار الخطي والانحدار اللوجستي بطريقة مشابهة جدًا.
حسنًا ، رائع ، لدينا دالة تكلفة لتقليلها. حان الوقت لإطلاق الانحدار ، أليس كذلك؟
ليس بهذه السرعة – لاستخدام النسب المتدرجة ، نحتاج إلى معرفة التدرج اللوني لدالة التكلفة ، المتجه الذي يشير إلى اتجاه الانحدار الأكبر (نريد أن نتخذ خطوات متكررة في الاتجاه المعاكس للتدرج لنصل في النهاية إلى الحد الأدنى ).
باستثناء الشبكات العصبية ، لدينا العديد من الأوزان المتغيرة والتحيزات المترابطة جميعها. كيف نحسب انحدار كل ذلك؟ في القسم التالي ، سنرى كيف يساعدنا backpropagation في التعامل مع هذه المشكلة.
مراجعة سريعة للانحدار المتدرج
ال gradient للدالة هو المتجه الذي تكون عناصره مشتقات جزئية بالنسبة لكل معلمة. على سبيل المثال ، إذا كنا نحاول تقليل دالة التكلفة ، C (B0 ، B1) ، باستخدام معلمتين قابلتين للتغيير ، B0 و B1 ، فسيكون التدرج:
تدرج C (B0، B1) = [[dC / dB0] ، [dC / dB1]]
لذلك يخبرنا كل عنصر من عناصر gradient كيف ستتغير دالة التكلفة إذا طبقنا تغييرًا صغيرًا على تلك المعلمة المعينة – حتى نعرف ما يجب تعديله ومقدار التغيير. للتلخيص ، يمكننا السير نحو الحد الأدنى باتباع الخطوات التالية:
1- حساب ال gradient للشبكة العصبية (احسب ال gradient باستخدام قيم المعلمات الحالية).
2- القيام بتعديل كل معلمة بمقدار يتناسب مع عنصر التدرج الخاص بها وفي الاتجاه المعاكس لعنصر التدرج. على سبيل المثال ، إذا كان المشتق الجزئي partial derivative لدالة التكلفة بالنسبة إلى B0 موجبًا ولكنه صغير وكان المشتق الجزئي partial derivative بالنسبة إلى B1 سالبًا وكبيرًا ، فإنه يجب علينا تقليل B0 بمقدار ضئيل وزيادة B1 بمقدار كبير من أجل تقليل دالة التكلفة.
3- إعادة حساب التدرج باستخدام قيم المعلمات الجديدة المعدلة و تكرار الخطوات السابقة حتى الوصول إلى الحد الأدنى.
الإنتشار العكسي Backpropagation
تذكر أن الانتشار الأمامي Forward propagation هو عملية المضي قدمًا عبر الشبكة العصبية (من المدخلات إلى المخرجات النهائية أو التنبؤ). بينما ال Backpropagation هو العكس، فبمساعدته فإننا نعيد الخطأ error لا الاشارة signal إلى الوراء من خلال نموذجنا.
يوجد أدناه تصور لشبكة عصبية بسيطة حيث تنتشر البيانات من المدخلات إلى المخرجات. يمكن تلخيص العملية بالخطوات التالية:
1- يتم إدخال المدخلات في الطبقة الزرقاء من الخلايا العصبية وتعديلها بواسطة الأوزان weights والتحيز bias و دالة سيقمويد sigmoid في كل خلية عصبية للحصول على التنشيط activations. على سبيل المثال:
Activation_1 = Sigmoid (Bias_1 + W1 * Input_1)
Activation_1 و Activation_2 ، اللذان يخرجان من الطبقة الزرقاء ، يتم إدخالهما في العصبون الأرجواني ، الذي يستخدمهما لإنتاج تنشيط الإخراج النهائي final output activation.
والهدف من الانتشار الأمامي forward propagation هو حساب التنشيط activation في كل خلية عصبية لكل طبقة مخفية متتالية حتى نصل إلى المخرجات output.
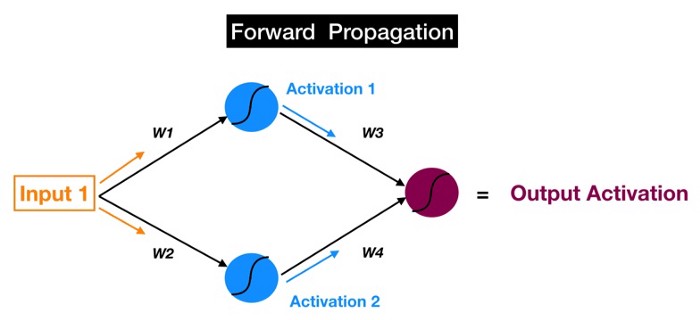
الآن دعونا نعكس الأمر. إذا اتبعت الأسهم الحمراء (في الصورة أدناه) ، فستلاحظ أننا نبدأ الآن في مخرج العصبون الأرجواني output of the magenta neuron. هذا هو تنشيط الإخراج output activation الخاص بنا ، والذي نستخدمه لعمل تنبؤاتنا ، والمصدر النهائي للخطأ في نموذجنا. نقوم بعد ذلك بنقل هذا الخطأ للخلف من خلال نموذجنا عبر نفس الأوزان والتوصيلات التي نستخدمها للإنتشار الأمامي لإشاراتنا (لذلك بدلاً من Activation 1 ، لدينا الآن Error1 – الخطأ المنسوب إلى الخلية العصبية الزرقاء العليا).
تذكر أننا قلنا أن الهدف من الانتشار الأمامي هو حساب تنشيط الخلايا العصبية طبقة تلو الأخرى حتى نصل إلى الناتج المرجوة يمكننا الآن تحديد هدف ال backpropagation بطريقة مماثلة:
نريد حساب الخطأ المنسوب إلى كل خلية عصبية بدءًا من الطبقة الأقرب إلى طبقة المخرجات وصولاً إلى البداية إلى طبقة المدخلات من نموذجنا.
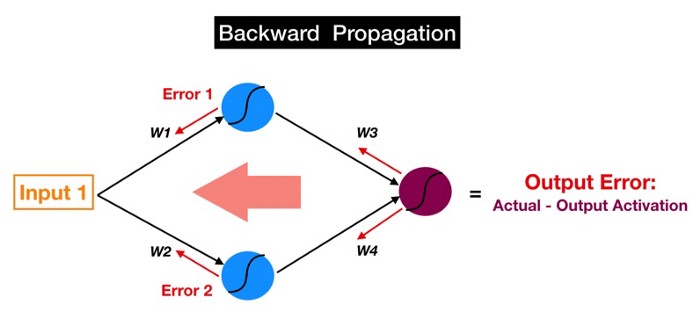
قد يتبادر الى أذهاننا السؤال التالي لماذا نهتم بالخطأ لكل خلية عصبية؟
للإجابة على ذلك تذكر أن اللبنتين الأساسيتين للشبكة العصبية هما الوصلات التي تمرر الإشارات إلى خلية عصبية معينة (مع وجود وزن weight لكل اتصال) والخلايا العصبية نفسها (مع وجود تحيز bias). هذه الأوزان والتحيزات عبر الشبكة بأكملها هي أيضًا مفاتيح التي نقوم بتعديلها لتغيير التنبؤات التي يقدمها النموذج.
هذا الجزء مهم حقًا:
يتناسب حجم الخطأ في خلية عصبية معينة (بالنسبة إلى أخطاء جميع الخلايا العصبية الأخرى) بشكل مباشر مع تأثير ناتج تلك الخلايا العصبية (مثل التنشيط activation) على دالة التكلفة cost function لدينا.
لذا فإن خطأ كل خلية عصبية هو يمثل ناتج للمشتق الجزئي partial derivatives لدالة التكلفة فيما يتعلق بمدخلات ذاك العصبون. هذا منطقي – إذا كان لدى خلية عصبية معينة خطأ أكبر بكثير من جميع الخلايا الأخرى ، فإن تعديل أوزان وتحيز الخلايا العصبية المخالفة سيكون له تأثير أكبر على الخطأ الكلي لنموذجنا من العبث بأي من الخلايا العصبية الأخرى.
والمشتقات الجزئية فيما يتعلق بكل وزن وتحيز هي العناصر الفردية التي تشكل متجه ال gradient لدالة التكلفة. لذلك يسمح لنا الانتشار العكسي backpropagation بشكل أساسي بحساب الخطأ المنسوب إلى كل خلية عصبية وهذا بدوره يسمح لنا بحساب المشتقات الجزئية partial derivatives وفي النهاية ال gradient حتى نتمكن من استخدام gradient descent.
مثال لتبسيط مبدأ عمل الإنشار العكسي – لعبة اللوم The Blame Game
كان لدى كل شخص منا في في مرحلة ما من حياته زميل فظيعشخص يلعب دائمًا لعبة إلقاء اللوم ويرمي زملاء العمل أو المرؤوسين تحت الحافلة عندما تسوء الأمور.
الخلايا العصبية ، عبر ال backpropagation ،تلعب نفس الدور في إلقاء اللوم. عندما ينتشر الخطأ إلى خلية عصبية معينة ، فإن تلك الخلية العصبية ستوجه الإصبع بسرعة إلى الخلية (أو الخلايا) التي في المنبع التي هو الأكثر خطأ و المتسببة في الخطأ (أي أن الخلايا العصبية من الطبقة 4 ستوجه الإصبع إلى الخلايا العصبية من الطبقة الثالثة ، و الخلايا العصبية من الطبقة الثالثة ستوجه الإصبع إلى الخلايا العصبية للطبقة الثانية ، وهكذا).
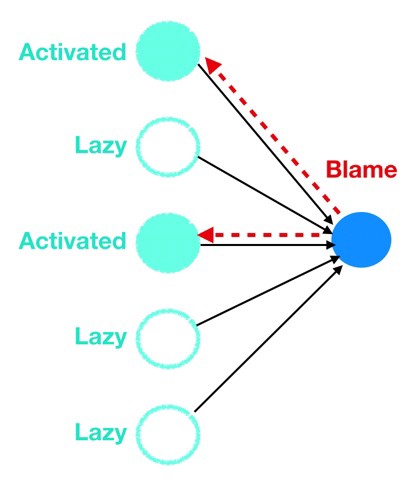
كيف تعرف كل خلية عصبية على من تلقي اللوم، لأن الخلايا العصبية لا تستطيع أن ترصد أخطاء الخلايا العصبية الأخرى بشكل مباشر؟ الإجابة بكل بساطة أن الخلايا تنظر فقط إلى من أرسل لهم أكثر إشارة من حيث عمليات التنشيط الأعلى والأكثر تكرارًا. تمامًا كما هو الحال في الحياة الواقعية ، فإن الأشخاص الكسالى الذين يلعبون بأمان (عمليات التنشيط المنخفضة وغير المتكررة) يتزلجون بدون لوم بينما يتم إلقاء اللوم على الخلايا العصبية التي تقوم بأكبر قدر من العمل وتعديل أوزانها وتحيزاتها. بالطبع هذه الطريقة تعتبر ساخرة لكنها أيضًا فعالة جدًا في الحصول على المجموعة المثلى من الأوزان والتحيزات التي تقلل من دالةالتكلفة لدينا.
في رأيي ، هذه هي النقاط الثلاثة الرئيسية للانتشار العكسي:
1- الإنتشار العكسي هي عملية تحويل الخطأ إلى الوراء طبقة تلو الأخرى وإسناد مقدار الخطأ الصحيح إلى كل خلية عصبية في الشبكة العصبية.
2- الخطأ المنسوب إلى خلية عصبية معينة هو تقريب جيد لكيفية تأثير تغيير أوزان تلك الخلايا العصبية (من الوصلات المؤدية إلى الخلية العصبية) والتحيز على دالة التكلفة.
3- عند النظر إلى الوراء ، فإن الخلايا العصبية الأكثر نشاطًا (الخلايا غير الكسولة) هي تلك التي يتم إلقاء اللوم عليها وتعديلها بواسطة عملية الإنتشار العكسي.
كيف تتعلم الشبكات العصبية
على عكس الخوارزميات الأخرى ، لا يمكن برمجة و تطبيق الشبكات العصبية بتعلمها العميق مباشرة على المهام المناطة بحلها لأنها بحاجة إلى تعلم المعلومات ، تمامًا مثل دماغ الطفل النامي. تمر استراتيجيات التعلم بثلاث طرق:
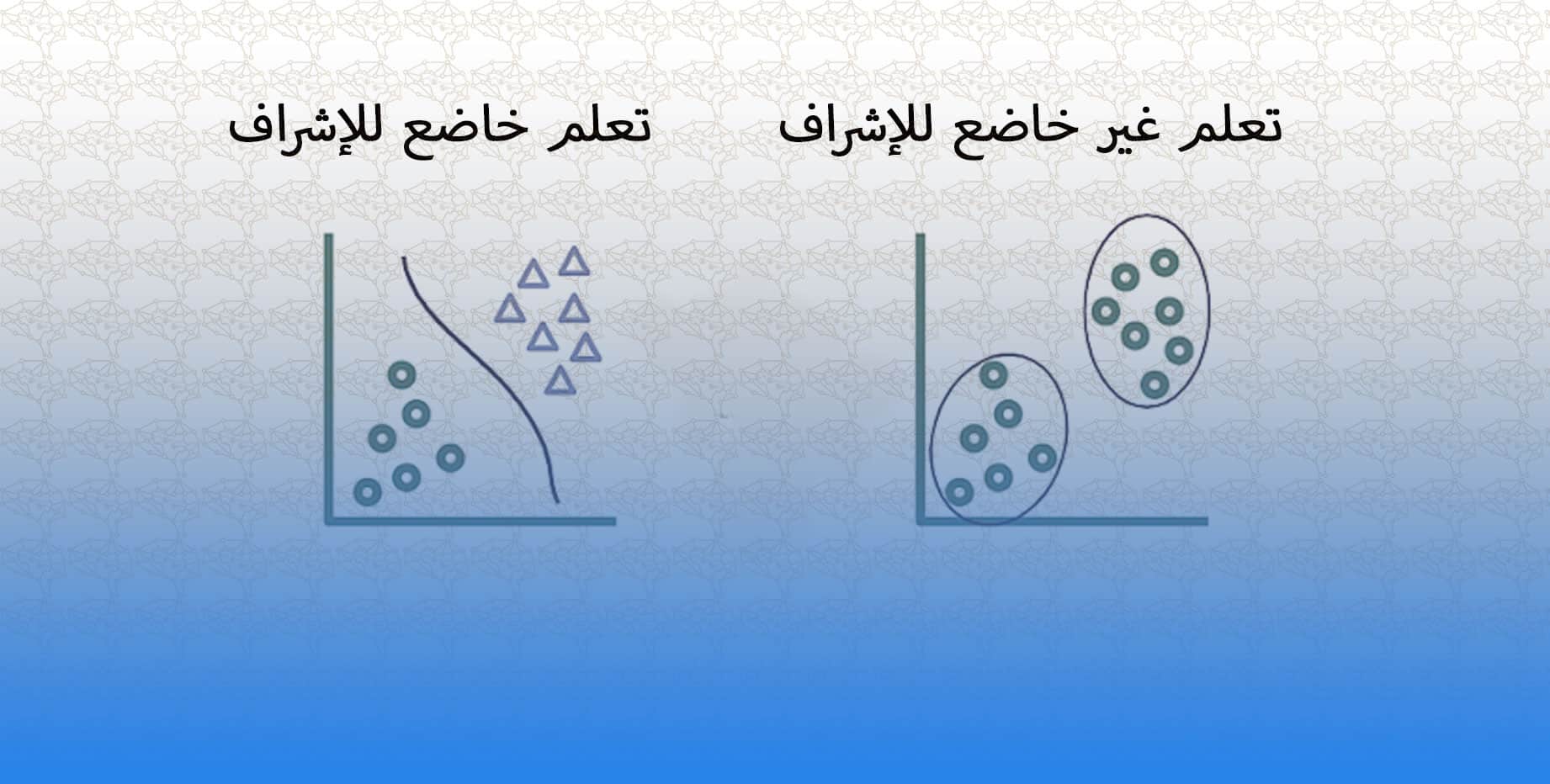
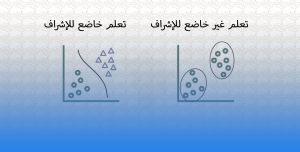
التعلم الخاضع للإشراف: استراتيجية التعلم هذه هي الأبسط ، حيث توجد مجموعة بيانات معنونة بيانات مدخل و بيانات مخرج و مقسمة إلى بيانات تدريب و بيانات إختبار ، يمر بها الكمبيوتر ، ويتم تعديل الخوارزمية حتى تتمكن من معالجة مجموعة البيانات للحصول على النتيجة المرجوة.
التعلم غير الخاضع للإشراف: تُستخدم هذه الاستراتيجية في الحالات التي لا توجد فيها مجموعة بيانات مصنفة متاحة للتعلم منها. تقوم الشبكة العصبية بتحليل مجموعة البيانات ، ثم تقوم دالة التكلفة cost function بإخبار الشبكة العصبية بمدى بُعدها عن الهدف. ثم يتم تعديل الشبكة العصبية لزيادة دقة الخوارزمية.
التعلم المعزز: في هذه الخوارزمية ، يتم تعزيز الشبكة العصبية للحصول على نتائج إيجابية ، ويتم معاقبتها على نتيجة سلبية ، مما يجبر الشبكة العصبية على التعلم بمرور الوقت.
إستخدامات الشبكات العصبيىة في حياتنا اليومية
التعرف على خط اليد هو مثال بسيط و شائع لما يمكن للشبكة العصبية الاصطناعية التعامل معه في إستخداماتنا اليومية. التحدي هو أن البشر يمكنهم التعرف على الكتابة اليدوية بحدس بسيط ، لكن التحدي الذي يواجه أجهزة الكمبيوتر هو أن الكتابة اليدوية لكل شخص فريدة من نوعها ، مع أنماط مختلفة ، وحتى تباعد مختلف بين الحروف ، مما يجعل من الصعب التعرف عليها باستمرار.
على سبيل المثال ، يمكن وصف الحرف الأول ، وهو حرف كبير A ، على أنه ثلاثة خطوط مستقيمة حيث يلتقي اثنان عند القمة في الجزء العلوي ، والثالث عبر الحرفين الآخرين في منتصف الطريق لأسفل ، ويكون منطقيًا للبشر ، ولكنه يمثل تحدي التعبير عن هذا في خوارزمية الكمبيوتر.
من خلال اتباع نهج الشبكة العصبية الاصطناعية ، يتم تغذية الكمبيوتر بأمثلة تدريبية لأحرف مكتوبة بخط اليد معروفة ، والتي تم تصنيفها مسبقًا على أساس الحرف أو الرقم الذي تتوافق معه ، ومن خلال الخوارزمية ، يتعلم الكمبيوتر بعد ذلك التعرف على كل حرف ، وكبيانات يتم زيادة مجموعة الأحرف ، وكذلك الدقة. التعرف على خط اليد له تطبيقات مختلفة ، مثل القراءة الآلية للعناوين على الرسائل في الخدمة البريدية ، مما يقلل الاحتيال المصرفي على الشيكات ، إلى إدخال الأحرف للحوسبة القائمة على القلم.
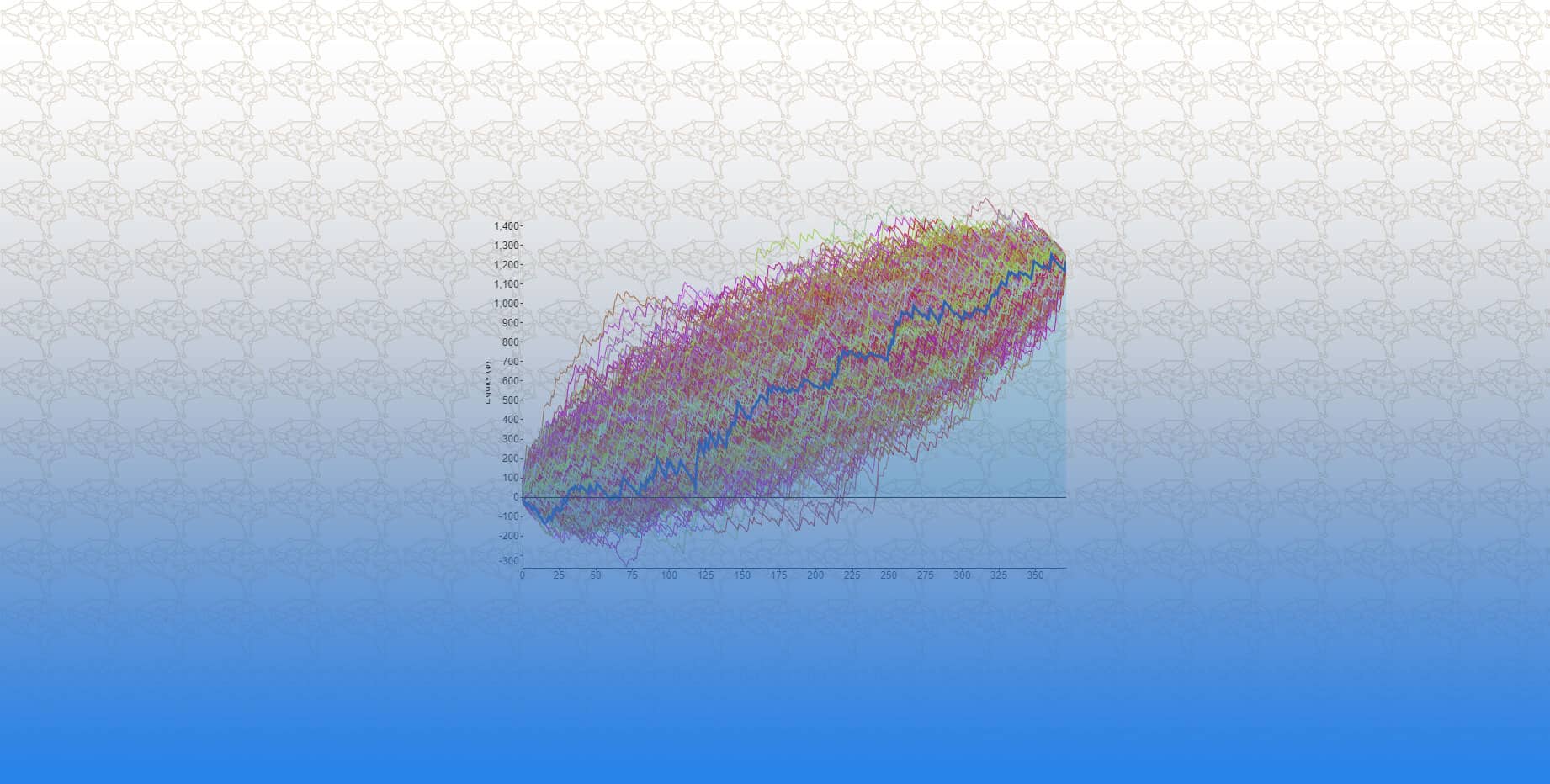
إستخدام آخر للشبكات العصبية الاصطناعية هو التنبؤ بالأسواق المالية. ينطبق هذا أيضًا على مصطلح “التداول الخوارزمي” ، وقد تم تطبيقه على جميع أنواع الأسواق المالية ، من أسواق الأسهم والسلع وأسعار الفائدة والعملات المختلفة. في حالة سوق الأوراق المالية ، يستخدم المتداولون خوارزميات الشبكة العصبية للعثور على الأسهم ذو الأقل القيمة ، وتحسين نماذج الأسهم الحالية ، واستخدام جوانب التعلم العميق لتحسين الخوارزميات الخاصة بهم مع تغير السوق. هناك الآن شركات متخصصة في خوارزميات تداول أسهم الشبكة العصبية ، على سبيل المثال ، MJ Trading Systems.
يستمر تطبيق خوارزميات الشبكة العصبية الاصطناعية ، بمرونتها المتأصلة ، في التعرف على الأنماط المعقدة ومشكلات التنبؤ. بالإضافة إلى الأمثلة المذكورة أعلاه ، يتضمن ذلك تطبيقات متنوعة مثل التعرف على الوجه على صور وسائل التواصل الاجتماعي ، واكتشاف السرطان للتصوير الطبي ، والتنبؤ بالأعمال.
المصادر: