خوارزمية انحدار المتجة الداعم (SVٌR) هي خوارزمية تعلم آلي تُستخدم لتحليل الانحدار ، والتي تتضمن التنبؤ بالقيم العددية المستمرة. أيضا هي تندرج تحت خوارزمية آلة المتجهات الدعمة (SVM) ، الخوارزمية المعروفة الاستخدام لمهام التصنيف و التنبؤ. بعد الإنتهاء من هذا المقال ستكون قادر على فهم خوارزمية انحدار المتجة الداعم.
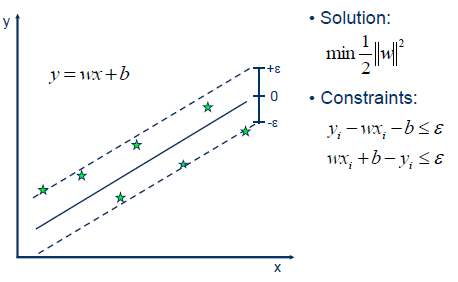
في خوارزمية انحدار المتجه الداعم ، الهدف هو ملاءمة خط الانحدار الذي يفصل البيانات على أفضل وجه إلى فئتين ، حيث تمثل إحدى الفئات المتغير المستهدف ، بينما تمثل الفئة الأخرى الأخطاء المتبقية. يمثل خط الانحدار هذا المستوى الفائق الذي يزيد الهامش بين المتغير الهدف والأخطاء المتبقية. يتم تعريف الهامش على أنه المسافة بين المستوى الفائق وأقرب نقاط البيانات ، والمعروفة باسم متجهات الدعم. التعامل مع العلاقات غير الخطية بين المتغيرات المستقلة والتابعة ويمكنها أيضًا التعامل مع القيم المتطرفة بشكل فعال. هذا يجعل خوارزمية انحدار متجة الدعم مفيدة لمهام التنبؤ المختلفة ، مثل التنبؤ بأسعار الأسهم ، والتنبؤ بالطقس. باختصار ،تعتبر خوارزمية انحدار متجه الدعم خوارزمية تعلم آلي قوية ومرنة ، خاصةً عندما تحتوي البيانات على علاقة غير خطية أو قيم متطرفة.
كيف تعمل خوارزمية انحدار المتجه الداعم؟
تحافظ خوارزمية انحدار المتجه الداعم على جميع الخصائص المثيرة للاهتمام في خوارزمية آلة المتجهات الداعمة. بحيث يتم استخدام نفس المبادئ التي يتم استخدامها في خوارزمية ألة المتجهات الداعمة للتصنيف، مع بعض الاختلافات الطفيفة فقط. استنادا إلى البيانات المدرجة، فإن هذه الطريقة تحاول إيجاد منحنى. ومع ذلك ، فبدلاً من أن يكون المنحنى بمثابة حدود للقرار في مسألة التصنيف، في خوارزمية انحدار المتجه الداعم SVR ، يتم ايجاد تطابق بين بعض المتجهات والموضع على المنحنى. ومع ذلك ، فإن الفكرة الرئيسية هي نفسها دائمًا: تقليل نسبة الخطأ في النتائج، وتخصيص المستوى الفائق الذي يزيد من قيمة الهامش إلى أقصى حد ، مع مراعاة أن جزءًا من الخطأ مسموح به.
التشابه بين SVM و SVR
خوارزمية انحدار المتجه الداعم SVR تشارك خوارزمية المتجهات الدعمة في إيجاد أقرب تطابق بين نقاط البيانات والدالة الفعلية التي تمثلها. بشكل تلقائي، عندما نزيد المسافة بين المتجهات الداعمة إلى المنحنى المتراجع ، فإننا نقترب من المنحنى الفعلي (نظرًا لوجود بعض الاخطاء دائمًا في العينات الإحصائية). ويترتب على ذلك أيضًا أنه يمكننا التخلص من جميع المتجهات التي ليست متجهات داعمة، لسبب بسيط هو أنها من المحتمل أن تكون قيم إحصائية متطرفة.
النواة Kernal و خوارزمية انحدار المتجه الداعم SVR
يمكنن تطبيق طريقة النواة في خوارزمية انحدار المتجه الداعم SVR أيضا. وبالتالي، من الممكن ان معالجة انحدار أي دالة غير خطية، أو منحنى باستخدام خوارزمية انحدار المتجه الداعم SVR. و بالمثل، يتم تعيين البيانات غير الخطية على مساحة تجعل البيانات خطية. في حالة خوارزمية انحدار المتجه الداعم SVR، لا يلزم أن تكون خطية من أجل فصل مجموعتين ، بل لتمثيل خط مستقيم وبالتالي حساب مساهمة متجهات الدعم في مسألة التنبؤ.
أنواع خوارزمية انحدار المتجه الداعم SVR
هناك عدة أنواع من خوارزمية انحدار المتجه الداعم SVR بناءا على نوع النواة المستخدمة لنمذجة العلاقة بين المتغيرات ، بما في ذلك:
- انحدار المتجه الداعم ذو النواة الخطية: يستخدم هذا النوع من خوارزمية انحدار المتجه الداعم نواة خطية لنمذجة العلاقة بين المتغيرات.
- انحدار المتجه الداعم ذو النواة متعدد الحدود: يستخدم هذا النوع من انحدار المتجه الداعم نواة متعددة الحدود لنمذجة العلاقة غير الخطية بين المتغيرات.
- انحدار المتجه الداعم ذو نواة دالة الأساس الشعاعي (RBF): يستخدم هذا النوع من انحدار المتجه الداعم نواة دالة الأساس الشعاعي لنمذجة العلاقة غير الخطية بين المتغيرات. دالة الأساس الشعاعي هي واحدة من أكثر النوى شيوعًا المستخدمة في انحدار المتجه الداعم.
- انحدار المتجه الداعم ذو نواة دالة سيجمويد: يستخدم هذا النوع من انحدار المتجه الداعم نواة دالة سيجمويد لنمذجة العلاقة غير الخطية بين المتغيرات.
- انحدار المتجه الداعم ذو نواة الشبكة العصبية ANN: يستخدم هذا النوع من انحدار المتجه الداعم الشبكات العصبية الاصطناعية لنمذجة العلاقة بين المتغيرات.
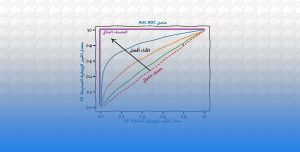
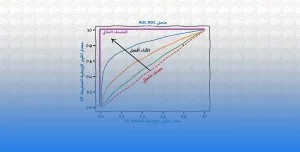
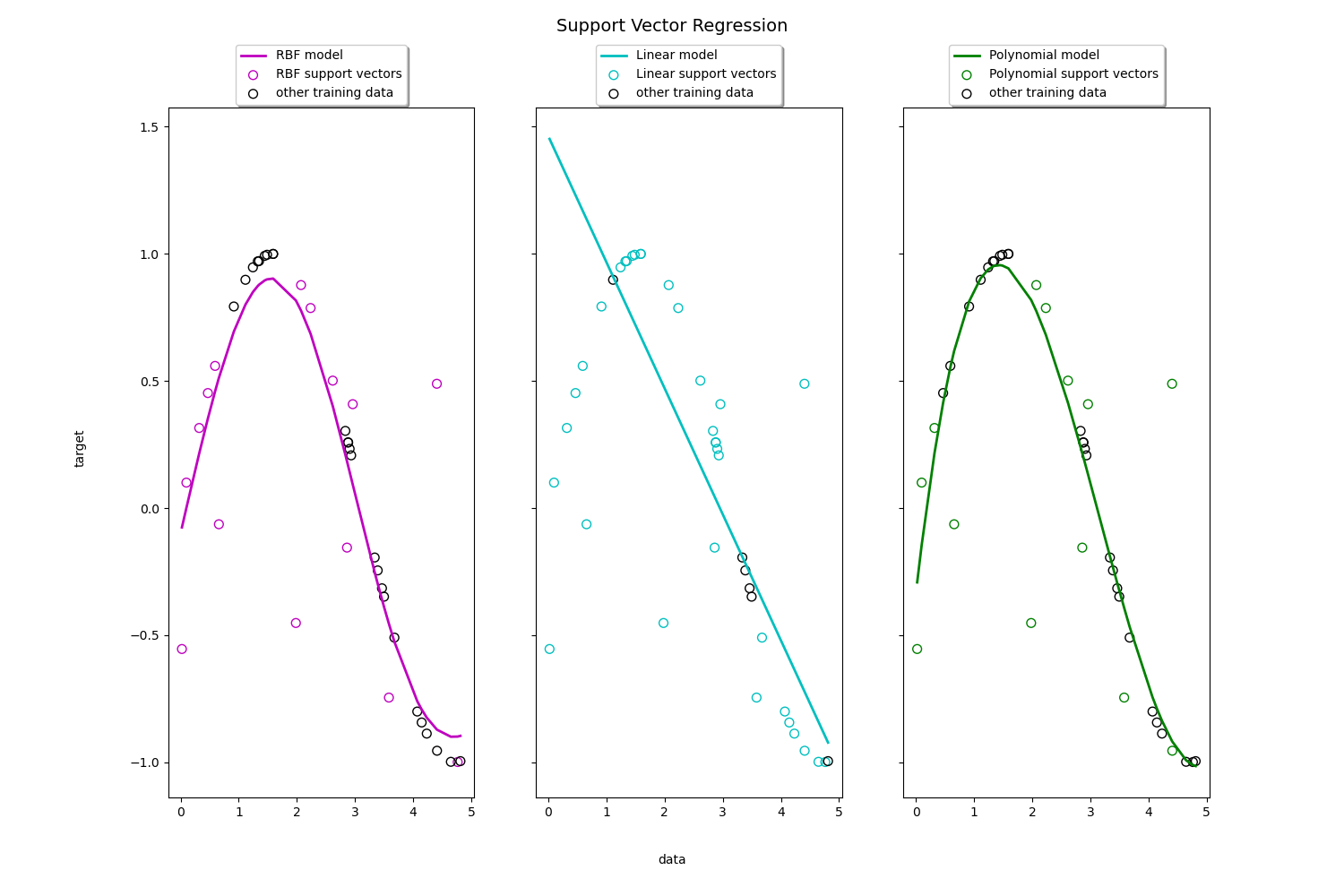
لكل نواة من نوى انحدار المتجه الداعم نقاط قوة و نقاط ضعف خاصة بها ويعتمد اختيار النواة المناسبة على طبيعة البيانات والمشكلة التي يتم حلها. في الأشكال أدناه نرى النماذج المختلفة لخوارزمية انحدار المتجه الداعم: الخطي ، دالة الأساس الشعاعي (RBF) ، متعددة الحدود.
-
انحدار المتجه الداعم الخطي (Linear SVR)

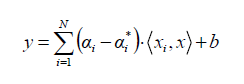
-
انحدار المتجه الداعم غير خطي (Non-linear SVR)
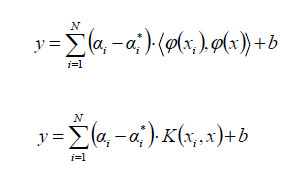

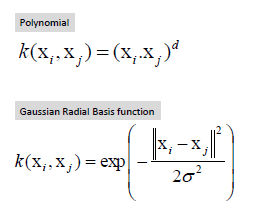
مثال عملي في لغة البرمجة بايثون
في معظم نماذج الانحدار الخطي البسيط ، يكون الهدف الرئيسي هو تقليل نسبة الخطاء. اذا أخذنا المربعات الصغرى الخطية OLS على سبيل المثال. إن دالة الهدف لـ OLS مع ميزة أو خاصية واحدة يمكن وصفها كالتالي:
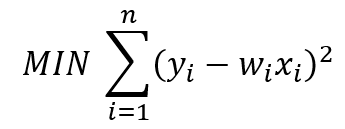
حيث yᵢ هو الهدف ، و w هو معامل الوزن ، و xᵢ هي الميزة او الخاصية.
يمنحنا انحدار المتجه الداعم المرونة لتحديد مقدار الخطأ المقبول في النموذج الذي نعمل عليه وسيجد خطًا مناسبًا (أو سطحًا فائقًا بأبعاد أعلى) لملاءمة البيانات.
الفرق بين SVR و OLS
على عكس OLS ، فإن الهدف الرئيسي من انحدار المتجه الداعم هو تقليل المعاملات – وبشكل أكثر تحديدًا ، معيار-L2 (L2-norm) لمتجه المعامل ) يحسب المعيار L2 مسافة إحداثيات المتجه من أصل مساحة المتجه. على هذا النحو ، يُعرف أيضًا باسم المعيار الإقليدي حيث يتم حسابه على أنه المسافة الإقليدية من الأصل. تكون النتيجة قيمة مسافة موجبة (- وليس للخطأ التربيعي. بدلاً من ذلك ، يتم التعامل مع الخطأ بصرامة و بقيود، حيث نقوم بتعيين الخطأ المطلق أقل من أو يساوي هامش محدد ، يسمى الحد الأقصى للخطأ، .ϵ (epsilon) يمكننا ضبط إبسيلون للحصول على الدقة المطلوبة للنموذج. الدالة و القيود الموضوعية الجديدة هي كما يلي:
دالة الفقد Minimize.
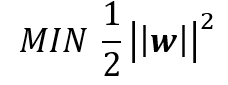
ضمن الحدود Constraints
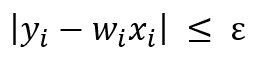
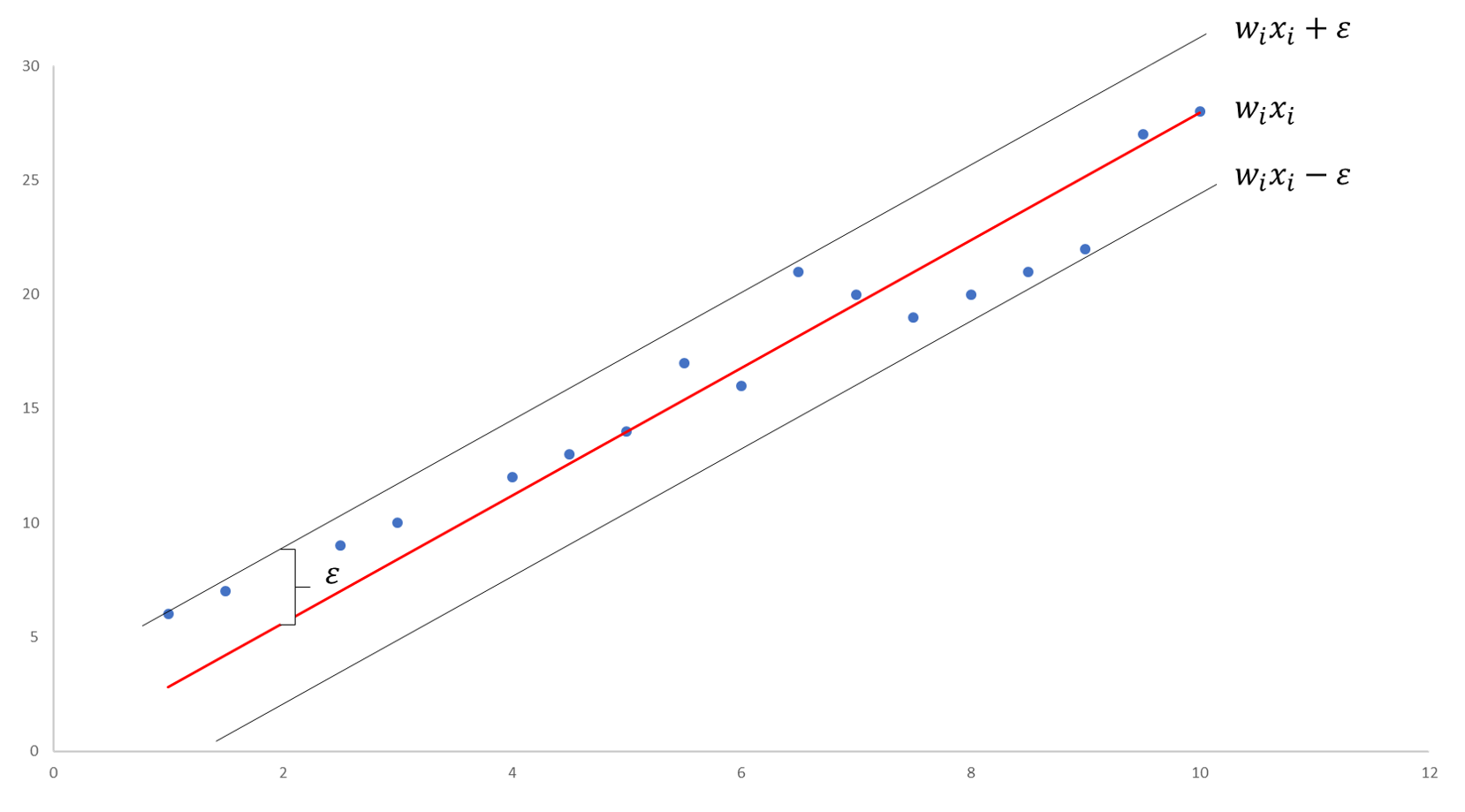
رسم توضيحي لانحدار المتجه الداعم SVR البسيط
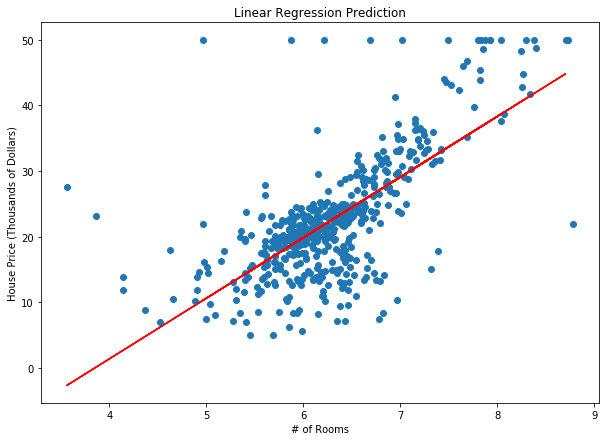
دعنا نجرب طريقة انحدار المتجه الداعم SVR البسيط في مجموعة البيانات التالية. يوضح المخطط أدناه نتائج نموذج انحدار المتجه الداعم SVR البسيط المدرب على بيانات أسعار الإسكان في مدينة بوسطن. الخط الأحمر يمثل الخط الأكثر ملاءمة والخطوط السوداء تمثل هامش الخطأ ، ϵ ، الذي قمنا بتعيينه إلى 5 (5000 دولار).
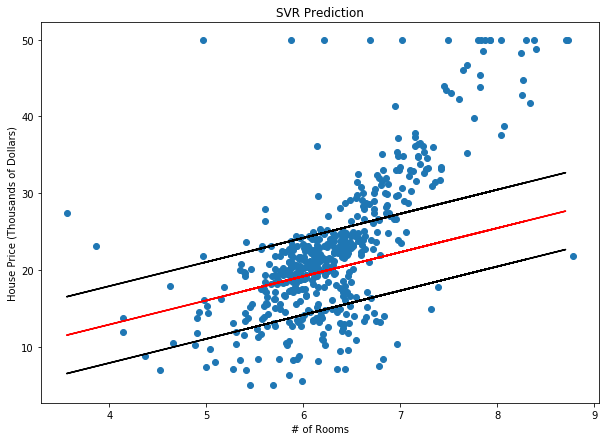
توقع انحدار المتجه الداعم SVR لأسعار المساكن في بوسطن مع قيمة ϵ تساوي 5
دالة الفقد مع متغيرات الركود
قد تدرك بسرعة أن هذه الخوارزمية لا تعمل مع جميع نقاط البيانات. حلت الخوارزمية دالة الهدف بأفضل طريقة ممكنة ولكن بعض النقاط لا تزال تقع خارج الهوامش. على هذا النحو ، نحتاج إلى حساب احتمال أخطاء أكبر من ϵ. يمكننا القيام بذلك مع متغيرات الركود. مفهوم متغيرات الركود بسيط: بالنسبة لأي قيمة تقع خارج ϵ ، يمكننا أن نشير إلى انحرافها عن الهامش كـ ξ. نحن نعلم أن هذه الانحرافات وجودها معقول ، ولكننا ما زلنا نرغب في تقليلها قدر الإمكان. وبالتالي ، يمكننا إضافة هذه الانحرافات إلى الدالة الموضوعية أو دالة الفقد .
دالة الفقد Minimize
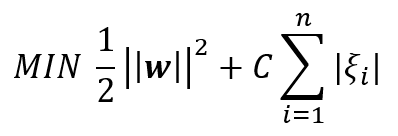
الحدود Constraints
![]()

مثال توضيحي لـ انحدار المتجه الداعم SVR مع متغيرات الركود Slack
لدينا الآن مستوى فائق إضافي C ، يمكننا ضبطه. كلما زادت قيمة المستوى C ، زادت احتمالية وجود النقاط خارج جدود ϵ أيضًا. مع اقتراب C من 0 ، يقترب الاحتمال من 0 وتنهار المعادلة إلى المعادلة المبسطة (على الرغم من أنها غير ممكنة في بعض الأحيان).
دعونا نضع قيمة C = 1.0 ونعيد تدريب النموذج أعلاه. تم رسم النتائج أدناه:
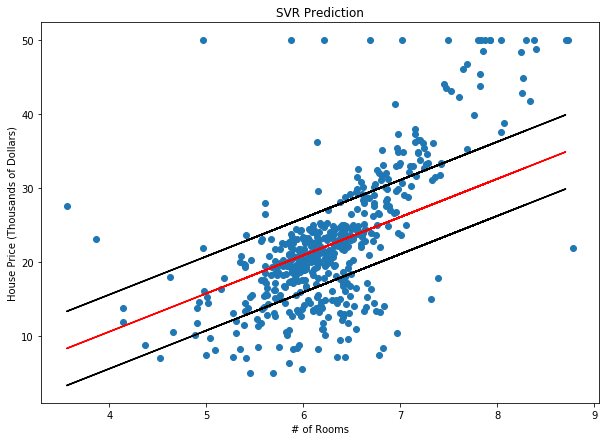
توقع انحدار المتجه الداعم SVR لأسعار المساكن في بوسطن مع ϵ = 5 ، C = 1.0
إيجاد أفضل قيمة لـ C
يبدو أن النموذج أعلاه قلل نسبة الخطأ نسبيا و أعطى نتائج أفضل من سابقه. يمكننا أن نخطو خطوة أخرى ونبحث على قيمة اخرى ل C للحصول على حل أفضل. لنفترض أن مقياس التقييم سيكون Within Epsilon%. يقيس هذا التقييم عدد النقاط الإجمالية ضمن مجموعة الاختبار التي تقع ضمن هامش الخطأ. يمكننا أيضًا مراقبة كيفية اختلاف متوسط الخطأ المطلق (MAE) مع قيمة C أيضًا.
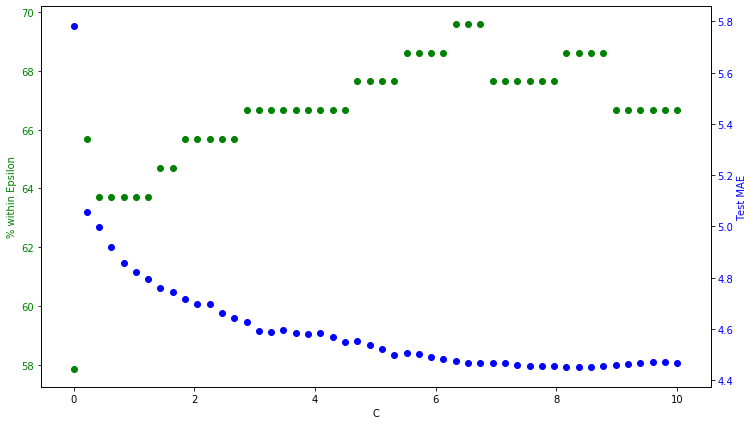
ايجاد قيمة C المثالية بناءا على قيمة within Epsilon% و متوسط الخطأ المطلق (MAE)
كما نرى ، تقل نسبة الخطأ MAE بشكل عام مع زيادة قيمة C. ومع ذلك ، نرى الحد الأقصى يحدث في تقييم within Epsilon%. و نظرًا لأن هدفنا الأصلي من هذا النموذج كان زيادة التنبؤ ضمن هامش الخطأ الذي حددناه (5000 دولار أمريكي) ، فإننا نريد ايجاد قيمة C التي تكون عندها قيمة within Epsilon% قصوى. وبالتالي قيمة C في هذه الحالة تساوي تقريبا 6.13. بناءا على هذه القيمة نبني نموذجًا أخيرًا باستخدام العوامل الفائقة النهائية ، ϵ = 5 ، C = 6.13.
يظهر الرسم البياني أعلاه أن هذا النموذج قد تحسن كثيرا مقارنة بالنماذج السابقة ، كما هو متوقع.
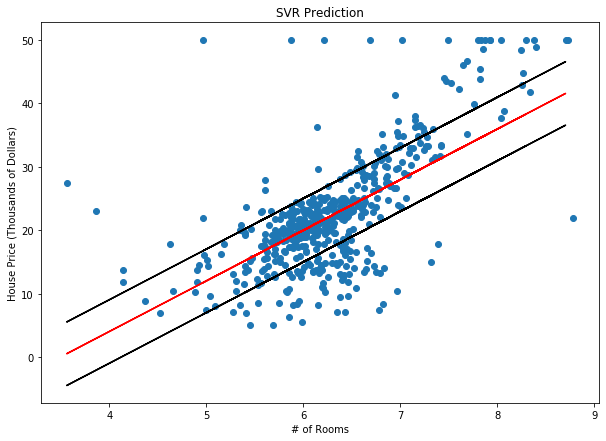
توقع انحدار المتجه الداعم SVR لأسعار المساكن في بوسطن مع ϵ = 5 ، C = 6.13
الكود المستخدم في لغة البرمجة بايثون
يمكن تحميل الكود كامل من خلال هذا الرابط هنا